【基本】関数の最大値・最小値
ここでは、一次関数を用いて、関数の最大値・最小値について見ていきます。
一次関数
x の一次式で表される関数を、x の一次関数(linear function)といいます。具体的な式で書くと、x の一次関数 y は次のようになります。\[ y=ax+b \]ここで、a, b は定数(x の値によって変わらない数)で、a は 0 以外とします。a が 0 のときは一次式にならないので、0 の場合は除きます。
一次関数 $y=ax+b$ のグラフは、直線になります。例えば、【基本】関数のグラフでも出てきましたが、 $y=2x-1$ のグラフは次のようになります。

このため、「一次関数 $y=ax+b$ のグラフ」のことを、「直線 $y=ax+b$ 」ということもあります。また、 $y=ax+b$ のことを、この直線の方程式といいます。
a は直線の傾き、b は(y 軸上の)切片といいます。
一次関数の値域
【基本】関数の復習#定義域と値域でも書きましたが、関数の「一部分だけ」を考えたいケースがあります。例えば、x が年齢を表しているときは、0 以上だけを考えたいですよね。
このように、関数の一部分だけを考えるとき、x の動く範囲を定義域、y の動く範囲を値域というのでした。具体的に、一次関数の場合で見てみましょう。
関数 $y=x+1 \ (1\leqq x \lt 3)$ の値域を考えてみます。
まず、定義域が実数全体の場合を考えます。この直線 $y=x+1$ は次のようになります。

今考えている関数では、定義域が $1\leqq x \lt 3$ なので、x軸上でいうと、次の部分のみを考えるということです。

青色の部分ですね。左端は含むので黒丸、右端は含まないので白丸にしています。【基本】一次不等式の解と数直線でみたかき方です。
この範囲に対応する関数のグラフは、次のように、太線の部分だけになります。

$y=x+1$ に $x=1$, $x=3$ と代入すると、それぞれ $y=2$, $y=4$ となるので、この範囲に対応するyの範囲は、次のように、y軸上の赤線の部分になります。
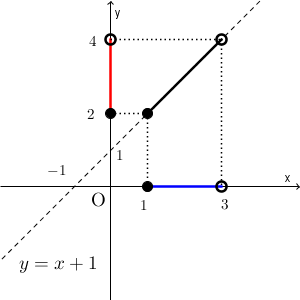
このことから、値域は、 $2\leqq y \lt 4$ となります。
なお、「 $y=x+1 \ (1\leqq x \lt 3)$ のグラフをかきなさい」と言われたら、上の図から不要なものをとって、次のように答えます。

ポイントは3つあります。
- 関数のグラフ全体は破線で、対象の範囲は実線でかく。
- 範囲の端の座標を書く。
- 両端が含まれるかどうかを、黒丸・白丸で表す。
これは、定義域が一部分のときの一次関数のグラフのかき方ですが、他の関数のときも基本的にこのポイントを踏まえてかくことになります。今後、こういう事例が出てくるたびに紹介していきます。
関数の最大値と最小値
テレビで天気予報を見ると、天気や降水確率以外に、気温に関する予報もあります。時間帯ごとの気温の予報が伝えられることもありますが、最高気温と最低気温しか言わないことも多いです。一番高いところと低いところが重要なんですね。
関数も同じです。まずは、値が一番大きいところと一番小さいところを把握するのが大事です。
関数の値域(y の動く範囲)で一番大きな値のことを、この関数の最大値といいます。また、一番小さな値のことを、この関数の最小値といいます。
例えば、先ほど見た例 $y=x+1 \ (1\leqq x \lt 3)$ の最小値はいくらになるかというと、グラフを見てもわかる通り $2$ です。では、最大値はいくらになるかというと、 $4$ といいたいところですが、違うんですね。

値域というのは、「x が動いたときに、y がとり得る値の範囲」のことをいいます。今考えている範囲では $x\lt 3$ なので $y=x+1=4$ になる場合はないんですね。 $4$ にすごく近い値はとるんだけど、 $4$ そのものにはなりません。
では、このときの最大値は何かというと、「最大値はない」が正解になります。「 $4$ より小さくて $4$ に一番近い値」を具体的な数で言うことはできないので、「ない」が答えになります。いじわる問題みたいですね。
また、関数 $y=x+1 \ (x\geqq 1)$ の場合も、最大値はありません。x はどこまでも大きな数をとることができるので、y もとても大きな数になりえます。「一番大きな数」というのはないので、この場合も「最大値はない」が正解になります。
最大値・最小値を聞かれた場合、「y がその値になるような x があるのか」は重要です。そのため、「その値になる x の値」も一緒に答えるのが一般的です。
たとえば、「 $y=x+1 \ (1\leqq x \lt 3)$ の最大値・最小値を求めなさい」と言われれば、次のように解答しましょう。
最大値はない
$x=1$ のとき、最小値 $2$ をとる
また、ケースにもよりますが、(グラフをかけと言われてなくても)グラフもかいて解答するのが一般的です。答えだけをかく場合でも、グラフをかいて考えるようにしましょう。グラフをかいたほうが、間違いに気づきやすくなります。
おわりに
ここでは、一次関数を使って、関数の最大値・最小値を見てきました。今後いろんな関数が出てきて、そのたびに最大値・最小値は考えることになります。ここの内容はすごく基本的なので、おさえておきましょう。





