【基本】増減表

🕒 2017/10/17 🔄 2023/05/01

ここでは、微分を用いて、増減表を書く方法、そして、グラフの概形をかく方法を見ていきます。なお、ここで出てくる関数は、整式で表されるものを想定しています。

📘 目次

微分と関数の増減に関する復習

【基本】微分と関数の増減でも見た内容ですが、微分と関数の増減について、少し振り返っておきましょう。

ある点での関数の動きは、その点での接線の動きとほぼ同じになるのでした。それは接線の成り立ちを考えればわかります。2点を結んだ直線について、2点間の距離を縮めていったときに近づく直線が接線なので、逆にいえば、接点の近くでは関数と接線の動きはほぼ同じになるんでしたね。

また、接線の傾きは、その点での微分係数となるのでした。そこで、もし、ある区間で微分係数が正であれば、その区間での各点での接線の傾きが正であることから、もとの関数もどんどん値が増えていくことがわかります。このような「 x が増えるたびに関数の値が増えていく」ことを「単調に増加する」というのでしたね。

逆に、ある区間で微分係数がずっと負であれば、もとの関数は単調に減少することもわかります。

これらをまとめると、次のようになるのでした。

微分と関数の増減

ある区間で、つねに $f'(x)\gt 0$ ならば、 $f(x)$ はその区間で単調に増加する。
ある区間で、つねに $f'(x)\lt 0$ ならば、 $f(x)$ はその区間で単調に減少する。

これを使えば、導関数の符号を考えることで、どこからどこまで単調に増加し、どこからどこまで単調に減少するかがわかります。そのため、グラフの概形がかけるんですね。

実際に、かき方を見ていきましょう。

増減表

【導入】微分を考える意味についてで出てきた、 $y=2x^3-x$ という関数のグラフについて考えてみましょう。

まずは、先ほども見たように、導関数の符号を考えることが重要なのでしたね。導関数は、次のように計算できます。
\begin{eqnarray} y' &=& 6x^2-1 \end{eqnarray}よって、この「導関数のグラフ」は次のようになります。元の関数ではなくて、導関数のグラフ、であることに注意しましょう。

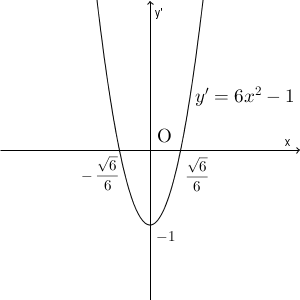
これは二次関数のグラフなのですぐにかけます。また、 x 軸との交点も、 $\left(\pm\dfrac{\sqrt{6} }{6},0\right)$ であることがわかります。

このグラフを見れば、 $x\lt -\dfrac{\sqrt{6} }{6}$ のときと、 $x\gt \dfrac{\sqrt{6} }{6}$ のときに、導関数が正になることがわかります。また、 $-\dfrac{\sqrt{6} }{6} \lt x \lt \dfrac{\sqrt{6} }{6}$ のときには、導関数が負になることがわかります。

このことと先ほど見た「微分と関数の増減」を見比べると、どの範囲で関数が増加して、どの範囲で減少するかがわかりますね。この対応は、次のような表にするとわかりやすいです。
\begin{array}{c|ccccc} x & \cdots & -\frac{\sqrt{6} }{6} & \cdots & \frac{\sqrt{6} }{6} & \cdots \\ \hline f’(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & \frac{\sqrt{6} }{9} & \searrow & -\frac{\sqrt{6} }{9} & \nearrow \end{array}この表は、増減表(first derivative test table) といいます。

この表は、次の順に埋まっていきます。まず、 $f'(x)$ のグラフから、どこで $f'(x)$ の符号が変わるか、符号はどうなるか、が決まります。つまり、1行目と2行目です。符号が分かれば、その区間での $f(x)$ の動きがわかるので、導関数がプラスなら関数は単調に増加するので「 $\nearrow$ 」を、マイナスなら単調に減少するので「 $\searrow$ 」をかきます。切り替わるときの関数の値は、計算するしかないので、最後に計算しておしまいです。

この増減表が作れれば、グラフの概形が分かったも同然です。途中に山と谷があることもわかります。グラフは次のようになります。