【基本】空間における直線や平面の決定

ここでは、空間における直線や平面の決定について見ていきます。

空間における直線の決定

平面の場合、ある2点を通る直線は、1つに決まります。定規を使って2点を結ぶことを考えれば、どう頑張っても1本しかひけないことがわかります。

空間の場合も、ある2点を通る直線は、1つに決まります。空間だと定規を使うことは難しいですが、例えば、糸でつなぐことを考えればイメージできると思います。糸をピンと張れば、2点を通る直線は1本しか引けないことがわかるでしょう。

空間における平面の決定

直線は2点を決めれば1つに決まりますが、平面を決めるには2点では足りません。

例えば、2本の指をL字にして、指先の上に下敷きを乗せたとしましょう。この状態ではフラフラとして、とてもバランスが悪いです。これは、平面が定まっていないことを表しています。

今度は3本の指を使って、指先が三角形の頂点になるようにしてみましょう。こうしてから下敷きを乗せれば、下敷きは安定します。これは、平面が定まったことを意味しています。

このように、平面が決まるには、3点が必要なことがわかります。

ただの3点ではいけません。この3点は同一直線上にあってはいけません。同一直線上にある場合は、やはり下敷きはフラフラとしてしまいます。

こうして、同一直線上にない異なる3点を決めれば、平面がただ1つに決まることがわかります。

また、以下のような条件でも、平面は1つに決まります。

• ある直線と、その直線上にない点
• 平行な（異なる）2直線
• 交わる2直線

まず1つ目の、「直線とその上にない点」とは、次のような状況です。

これは、直線の上に2点とれることから、「同一直線上にない異なる3点」を決めているのと本質的に同じです。

平行な2直線は、次のような状況です。

この場合も直線の上に2点とれるので、本質的に、「同一直線上にない異なる3点」を決めているのと同じです。

最後の交わる2直線も同様です。

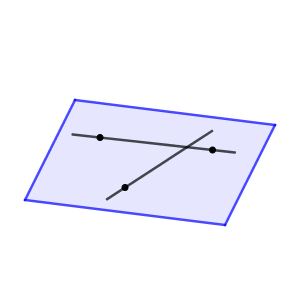
つまり、言い方が違っていますが、結局、同一直線上にない異なる3点を決めるような条件であれば、平面は1つに決めることができる、というわけです。

おわりに

ここでは、空間における直線や平面の決定について見てきました。平面を決めるには、同一直線上にない異なる3点を決めないといけない、という点をおさえておきましょう。