【基本】相関係数と散布図の関係

【基本】相関係数では、相関関係の強さを見るための指標である、相関係数を紹介しました。ここでは、相関係数の値と散布図を見比べて、相関係数について理解を深めていきます。

相関係数に関する復習

【基本】相関係数にも書いていることですが、簡単に復習しましょう。「正の相関関係がある」というのは、2つのデータを比べたときに「片方が大なら、もう片方も大」という関係があることをいうのでした。また、散布図をかいたときに、点の集まりが ある直線に近い場合は「強い相関」、そうでない場合は「弱い相関」というんでしたね。

散布図からこれらを判断するというのはあいまいだし、2つの散布図を比較するときに「見て判断」というのは少々不便です。なので、相関関係の強さを見るために、「相関係数」という指標を使います。相関係数には「 $-1$ 以上 $1$ 以下の値をとる」という性質があり、 $1$ に近い場合は、「強い正の相関がある」ということができます。

「あれ？　そんな話だったっけ？」と不安な人は、【基本】相関係数を見直してみましょう。

相関係数の値と散布図

さて、以下では、散布図とそれに対応する相関係数の値を見比べて、相関係数の値と散布図がどう関係しているかを、具体例で見ていきましょう。

まずは、 $r \fallingdotseq 0.9$ となる散布図の例です。 $0.9$ だと必ずこの散布図になる、というわけではありません。あくまでも一例です。

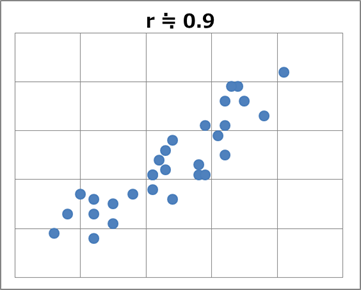
右肩上がりの直線に、かなりまとわりつくように分布していることがわかります。こういうときに、「強い相関がある」といいます。比較するために、 $r \fallingdotseq 0.7$ となる散布図の例を見てみましょう。

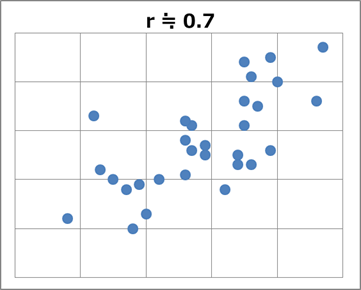
「片方が大なら、もう片方も大」という傾向は見えますが、初めの例より直線から離れる点が多いですね。

続いて $r \fallingdotseq 0.5$ となる散布図の例を見てみましょう。

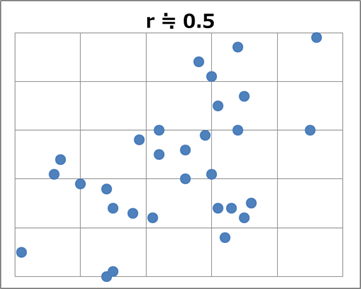
さきほどよりバラバラになっています。ここまでくると、「直線的に分布している」とはなかなかいいがたいです。 $r \fallingdotseq 0.3$ となる散布図の例を見ると、バラバラ度合いがさらに増します。

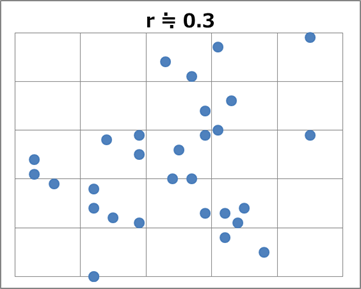
ここまでバラバラだと、「片方が大なら、もう片方も大」という傾向も怪しくなってきます。 $r \fallingdotseq 0.5$ のときと比べると、左下の点が減ったり、右下の点が増えたり、中央上側の点が増えたりしています。こういった「右肩上がりの直線から遠ざかる点」が増えると、相関係数は小さくなっていきます。

ここまでは、相関係数が正の場合を見てきましたが、ほぼ0という例も見てみましょう。

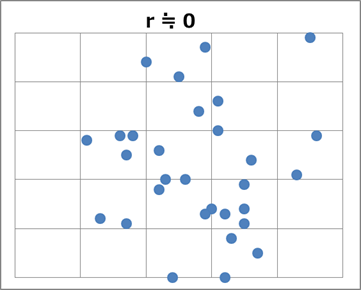
「片方が大なら、もう片方も大」も「片方が大なら、もう片方は小」も言えない感じですね。

散布図と相関係数の値を見比べてみると、相関係数が $1$ に近づくほど散布図は直線的になり、 $0$ に近づくほど散布図は全体的に点が散らばるようになる、ということがわかります。

相関係数は負の値にもなります。上の散布図を上下反転させたものが、負の場合の例となります。例えば、 $r \fallingdotseq 0.9$ の散布図の上下を反転すると、 $r \fallingdotseq -0.9$ の例になります。

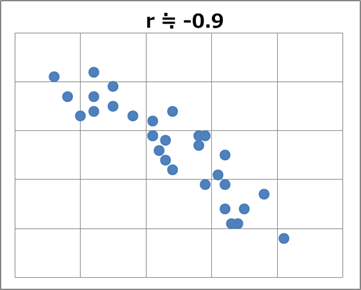
右肩上がりの直線だったところが、右肩下がりの直線に変わります。

おわりに

ここでは、散布図とそれに対応する相関係数を見比べて、相関係数の値によって散布図がどのように変わっていくかを見ました。 $0$ に近いほど直線的に分布し、 $0$ に近づいていくほど、直線から離れていくことがわかったと思います。

相関係数が、どの値から強い相関で、どの値から弱い相関なのか、というはっきりとした区切りはありません。「絶対値が $0.7$ 以上なら強い相関、$0.3$ ～ $0.5$ 程度なら弱い相関、それより小さい場合は相関がない」と判断されることが多いですが、あくまでも、目安でしかありません。実際に分析で使う場合には、相関係数と散布図とを並べて、相関の強さを判断することになります。