【基本】まとめて数える
ここでは、数え方の基本である「まとめて数える」方法を見ていきます。樹形図というものを利用して数えていきます。
書き出すときは辞書順で
ここでは、Aさん、Bさん、Cさん、Dさんの4人を1列に並べる方法は何通りあるかを考えてみます。
【基本】書き出して数えるで見たように、すべてのケースを書き出すのが基本です。少し書き出してみます。
- ABCD
- ABDC
- ACBD
- ACDB
- ADBC
- ADCB
なお、書き出すときには、モレやダブりがないように順番に並べることが重要です。上の並べ方は、2文字目がアルファベット順になっていて、2文字目が同じもの(例えばABCDとABDCなど)を比べると3文字目がアルファベット順になっています。
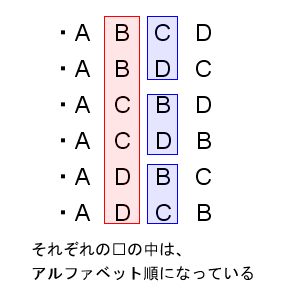
これは、紙の辞書と同じ並び順です。そのため、このような並び順を辞書順や辞書式順序(lexicographic order / dictionary order)と言います。またこのように並べることを辞書式に並べるとか辞書順に並べると言います。このように書きだすと、モレやダブりが発生することはありません。
樹形図を使って書きだそう
4人を並べる方法について、続けて考えていきましょう。
まだAさんが先頭の場合しか考えていませんでしたね。
- ABCD
- ABDC
- ACBD
- ACDB
- ADBC
- ADCB
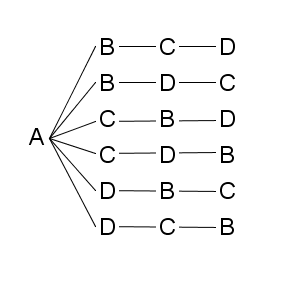
例えば上から3つ目は、「ACBD」という並び方に対応するということです。よく見ると、左から2番目もまとめることができますね。
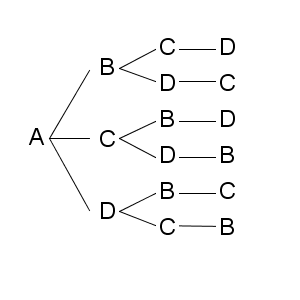
同じものをまとめるだけで、スッキリと書き出すことができます。このような図を樹形図(tree diagram)と言います。反時計回りに90度まわすと、木の幹から枝葉に分かれているような図になるので、こうした名前がついています。
まとめて数えよう
4人を並べる方法が何通りあるか、答えを出しましょう。大きな図になってしまいますが、すべてを樹形図で書き出すと、次のようになります。
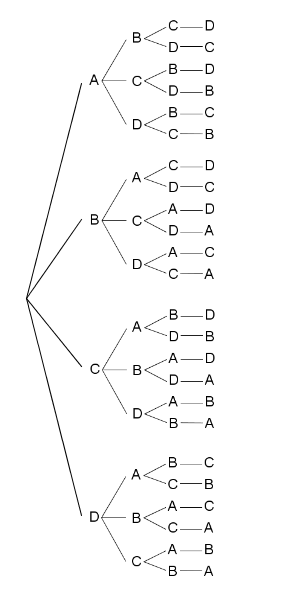
左側はまとめられているので、数えるときは右端の個数を数えます。全部で24通りであることがわかります。
しかし、右端を1個1個数えずに、まとめて数えたほうが楽チンです。先頭を決めた後の樹形図の構造は、次のようにすべて同じです。

赤い箱は4つあります。これは先頭の決め方が4通りあることに対応しています。また、赤い箱の中はすべて同じ構造なので、「 $4\times\bigcirc$ 」という式で計算できることがわかります。
次に赤い箱の中を考えてみましょう。1つ目の赤い箱の中は、次の部分が同じ構造になっています。
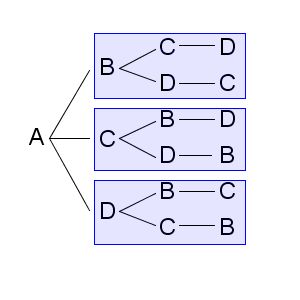
青い箱が3つあります。これは、2番目に並ぶ人の決め方が3通りあることに対応しています。青い箱の中はすべて同じ構造なので、全体の並び順は「 $4\times3\times\bigcirc$ 」という式で計算できることがわかります。
青い箱の中は、残りの2人を並べる方法なので、2通りです。以上から、\[ 4\times 3\times 2=24 \]通りと求めることができます。
この数え方は、樹形図で同じ構造のところをまとめて数えていることになります。同じことですが、次のように考えることもできます。先頭の決め方が4通りあり、それぞれに対して2番目の決め方が3通りあり、それぞれに対して、3番目の決め方が2通りあり、それぞれに対して4番目の決め方が1通りある。よって、\[ 4\times 3\times 2\times 1=24 \]通りと求められる、と。「それぞれに対して」というのは、樹形図でいうところの「それぞれの枝」に対応しています。はじめに4本の枝があって、それぞれの枝から3本ずつ枝が出て、それぞれの枝から2本ずつ枝が出て、最後に1本枝が出ている、ということですね。なので、掛け算をすれば、全体で何通りあるかが出てきます。
もし、4人ではなく5人を一列に並べる場合はどうなるでしょうか。先頭の決め方は5通りあります。先頭を決めた後の残りの4人の並び順の決め方は、今まで見てきたように24通りあります。先頭を決めると、その後にそれぞれ24通りの並び方ができるので、5人の並べ方は全部で\[ 5\times 24=120 \]通りとなります。樹形図でいうと、先頭に並ぶ人の右側に、上にかいた縦長の樹形図が続くことになるわけですね。
慣れてくると、樹形図をかかずに、計算式を使って場合の数を求めることができるようになります。ただ、「樹形図をかいたときに、同じ構造が出てくるから、掛け算で求めることができる」ということを、頭の片隅に入れておくようにしましょう。
おわりに
ここでは、樹形図と、まとめて数える方法の紹介をしました。毎回すべてのパターンを書き出すのは大変ですが、樹形図を使えば少し楽になります。また、樹形図をかいたときに、構造が同じ部分はまとめて数えることができるので、掛け算で答えを出すことができます。慣れてくれば、樹形図をかかなくても計算式が作れるようになりますが、頭の中では樹形図を思い描くようにしましょう。





