【基本】絶対値と数と大小

🕒 2019/04/08 🔄 2023/05/01

ここでは、正の数と負の数の大小を考えるときに、数直線を使わない方法について見ていきます。

📘 目次

数直線をかかずに数の大小を考えられるか

【基本】正負の数と大小では、 $+1$, $-3$, $-1.5$, $\dfrac{1}{2}$ の大小関係を数直線を使って考えました。

これより、\[ -3\lt -1.5 \lt \dfrac{1}{2} \lt +1 \]となることがわかります。

ただ、毎回数直線をかくのは面倒です。以下では、数直線を使わないで考える方法について見ていきます。

まず、正の数と負の数を比べたときに、正の数のほうが大きくなることはすぐにわかりますね。正の数は $0$ より大きく、負の数は、この基準の $0$ よりも小さいのだから、負の数は正の数よりも小さいです。このことは、数直線をかかなくてもわかります。

また、正の数同士の比較もできますね。 $+1$ と $\dfrac{1}{2}$ との比較は、符号をとって考えれば、小学校の算数でもやった内容です。 $+1$ のほうが大きいことがわかります。数字の部分が大きいほど、数直線では右に行く、つまり、より大きな数である、ということです。

ただ、負の数同士の比較は少し難しいですね。 $-3$ と $-1.5$ の比較はどうすればいいでしょう。これも、数直線をかかずに答えることはできないでしょうか。

正の数同士の比較では、符号をとって考えました。負の数同士の比較でも、符号をとって考えてみましょう。 $-3$, $-1.5$ は、符号をとると、それぞれ、 $3$, $1.5$ となります。数直線では、 $-3$ は $0$ よりも $3$ だけ左にあり、 $-1.5$ は $0$ よりも $1.5$ だけ左にあります。つまり、符号をとった後の数字の部分が大きい $-3$ のほうが、数直線上では、より左にあるということですね。このため、 $-3$ と $-1.5$ を比べると、 $-3$ のほうが小さいことがわかります。

絶対値

先ほど見た内容から、次のことがわかるでしょう。

まず、正の数は負の数よりも大きいです。また、数直線上で、正の数同士を比較すると、原点から遠いほど右にあるので、原点から遠いほど大きな数になります。一方、負の数同士を比較すると、原点から遠いほど左にあるので、原点から遠いほど小さな数になります。

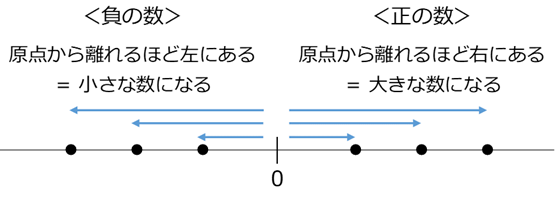
このことから、正の数同士や負の数同士の大小を考えるときには、原点からの距離を使うと便利そうですね。こうした便利なものには、名前がついています。絶対値(absolute value) といいます。 $+3$ も $-3$ も、原点から $3$ だけ離れているので、 $+3$ の絶対値も $-3$ の絶対値も $3$ となります。 $0$ の絶対値は $0$ です。

絶対値

数直線上で、ある数に対応する点と原点との距離を、絶対値という。

今の段階では、絶対値というのは、符号をとったものと同じになります。しかし、将来、符号をとるだけではダメな例も出てきます。絶対値とは、「数直線上での、原点からの距離だ」と理解しておきましょう。

少し、絶対値に関する例題を解いてみましょう。

例題1

$-10$, $+0.2$, $-0.3$, $-\dfrac{1}{3}$, $0$ の絶対値を、それぞれ答えましょう。

数直線上での、原点からの距離を答えることになるのですが、今の段階では、符号をとって考えればいいですね。絶対値は、それぞれ、 $10$, $0.2$, $0.3$, $\dfrac{1}{3}$, $0$ となります。これが答えです。

例題2

絶対値が $7$ となる数を答えましょう。

数直線上で、原点からの距離が $7$ となる数を答えればいいですね。右だけでなく左にもあることに注意しましょう。答えは、 $7$ と $-7$ の2つです。

絶対値と数の大小

ここまで見た内容から、次のことがわかるでしょう。

正負の数の大小と絶対値

正の数は負の数よりも大きい。
正の数は、絶対値が大きいほど、大きくなる。
負の数は、絶対値が大きいほど、小さくなる。

絶対値とは、数直線上での原点からの距離のことなので、絶対値が大きいほど原点から離れることになります。正の数であれば、絶対値が大きいほど右にあるということなので、より大きな数であることを表します。一方、負の数であれば、絶対値が大きいほど左にあるということなので、より小さな数であることを表します。

例題3

$-10$, $+0.2$, $-0.3$, $-\dfrac{1}{3}$, $0$ の大小を、不等号と使って表しなさい。

まずは、符号に着目して分類しましょう。

　正の数： $+0.2$
　$0$ ： $0$
　負の数： $-10$, $-0.3$, $-\dfrac{1}{3}$

となります。続いて、負の数の大小関係を考えます。数直線をかかなくても、絶対値を考えればいいのでしたね。負の数の絶対値を考えると、 $10$, $0.3$, $\dfrac{1}{3}$ となります。 $\dfrac{1}{3}=0.333\cdots$ となるので、絶対値の大小関係は\[ 0.3 \lt \frac{1}{3} \lt 10 \]となります。負の数の場合は、絶対値が大きいほど、小さい数を表すことから、\[ -0.3 \gt -\frac{1}{3} \gt -10 \]となります。全体では、\[ +0.2 \gt 0 \gt -0.3 \gt -\frac{1}{3} \gt -10 \]となります。これが答えです。