🏠 Home / 数学C / ベクトル

【基本】空間ベクトル

🕒 2024/06/30 🔄 2024/07/07

ここでは、空間ベクトルや空間ベクトルの演算などについて見ていきます。平面のときを思い出しながら見ていきます。

📘 目次

空間ベクトル

【基本】ベクトルで見たように、平面でのベクトルは、向きと大きさをもったもの、でした。空間ベクトルは、これを空間で考えるだけです。

空間内に2点 $\mathrm{A,B}$ をとります。 $\mathrm{A}$ から $\mathrm{B}$ の向きに、線分 $\mathrm{AB}$ と同じ長さの大きさをもつベクトルを $\overrightarrow{\mathrm{AB}}$ と表します。

$\overrightarrow{\mathrm{AB}}$ に対し、 $\mathrm{A}$ を始点、 $\mathrm{B}$ を終点と呼びます。

また、平面のときと同じように、一文字で $\vec{a}$ などと表すこともあります。

$\overrightarrow{\mathrm{AB}}$ の大きさとは、線分 $\mathrm{AB}$ の長さのことで、記号では $|\overrightarrow{\mathrm{AB}}|$ と表します。

2つのベクトルの向きと大きさが等しいとき、2つのベクトルは等しいといいます。

これらは、すべて平面のときと同じです。考えている場所が、平面から空間に変わっただけです。

空間ベクトルの足し算

【基本】ベクトルの足し算では、平面でのベクトルの足し算を見ました。しりとりのように計算する方法と平行四辺形を作る方法、2通りありましたが、結果は同じものになりました。

空間のときも同じように定義します。

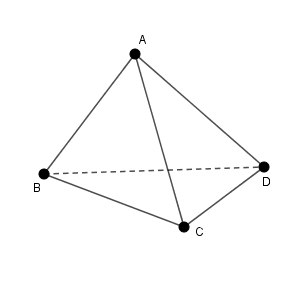
上のような四面体があったとします。このとき、\[ \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}} \]は、しりとりのように考えて、 $\overrightarrow{\mathrm{AC}}$ となります。この計算は空間で行っていますが、 $\mathrm{A,B,C}$ を含む平面での計算と考えれば、平面の計算とまったく同じことをしているとわかります。

$\overrightarrow{\mathrm{AB}}$ と $\overrightarrow{\mathrm{CD}}$ との和のような場合には、$\mathrm{C}$ が $\mathrm{A}$ や $\mathrm{B}$ にくるように $\overrightarrow{\mathrm{CD}}$ を平行移動するなどをしてから計算すればいいです。

交換法則 $\vec{a}+\vec{b}=\vec{b}+\vec{a}$ や、結合法則 $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$ も成り立ちます。

空間ベクトルの引き算

【基本】ベクトルの引き算で見た通り、平面の場合、 $\overrightarrow{\mathrm{AB}}$ ベクトルを引く場合は、 $\overrightarrow{\mathrm{BA}}$ を足す、と考えます。空間の場合も同じです。

上のような四面体があったとします。 $\overrightarrow{\mathrm{CD}} - \overrightarrow{\mathrm{AD}}$ を計算してみます。これは、後半の順番を変えて、符号も変えて\[ \overrightarrow{\mathrm{CD}} - \overrightarrow{\mathrm{AD}} = \overrightarrow{\mathrm{CD}} + \overrightarrow{\mathrm{DA}} = \overrightarrow{\mathrm{CA}} \]となります。

$\overrightarrow{\mathrm{BA}}$ は $\overrightarrow{\mathrm{AB}}$ の逆ベクトルといいます。ベクトルを引く場合は、逆ベクトルを足すことで求めます。

$\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{AB}}$ や $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BA}}$ は、長さが $0$ のベクトルとなります。これは特別に零ベクトルという名前がついていて、 $\vec{0}$ で表します。