東京大学 理系 2023年度 第6問 解説

問題編

問題

　$\mathrm{O}$ を原点とする座標空間において、不等式 $|x|\leqq 1$, $|y|\leqq 1$, $|z|\leqq 1$ の表す立方体を考える。その立方体の表面のうち、 $z\lt 1$ を満たす部分を $S$ とする。

　以下、座標空間内の2点 $\mathrm{A,B}$ が一致するとき、線分 $\mathrm{AB}$ は点 $\mathrm{A}$ を表すものとし、その長さを $0$ と定める。

(1) 座標空間内の点 $\mathrm{P}$ が次の条件(i), (ii) をともに満たすとき、点 $\mathrm{P}$ が動きうる範囲 $V$ の体積を求めよ。

　(i) $\mathrm{OP}\leqq \sqrt{3}$
　(ii) 線分 $\mathrm{OP}$ と $S$ は、共有点を持たないか、点 $\mathrm{P}$ のみを共有点に持つ。

(2) 座標空間内の点 $\mathrm{N}$ と点 $\mathrm{P}$ が次の条件(iii), (iv), (v) をすべて満たすとき、点 $\mathrm{P}$ が動きうる範囲 $W$ の体積を求めよ。必要ならば、 $\sin\alpha=\dfrac{1}{\sqrt{3}}$ を満たす実数 $\alpha$ $\left(0\lt \alpha\lt\dfrac{\pi}{2} \right)$ を用いてよい。

　(iii) $\mathrm{ON+NP}\leqq \sqrt{3}$
　(iv) 線分 $\mathrm{ON}$ と $S$ は共有点を持たない。
　(v) 線分 $\mathrm{NP}$ と $S$ は、共有点を持たないか、点 $\mathrm{P}$ のみを共有点に持つ。

考え方

(1)はまだイメージがつきやすいですが、(2)はそもそもどの部分の体積を求めればいいかがわかりにくいです。追加で新しく動けるようになった部分を考えるようにします。

1回曲がってもよくなったことで、(1)のときよりも立方体の外側にいけるようになります。使える道具は積分くらいなので、どういう断面で切るか、断面がどうなっているかを考えましょう。時間内に解ききるのはかなり難しいです。

解答編

問題

　$\mathrm{O}$ を原点とする座標空間において、不等式 $|x|\leqq 1$, $|y|\leqq 1$, $|z|\leqq 1$ の表す立方体を考える。その立方体の表面のうち、 $z\lt 1$ を満たす部分を $S$ とする。

　以下、座標空間内の2点 $\mathrm{A,B}$ が一致するとき、線分 $\mathrm{AB}$ は点 $\mathrm{A}$ を表すものとし、その長さを $0$ と定める。

(1) 座標空間内の点 $\mathrm{P}$ が次の条件(i), (ii) をともに満たすとき、点 $\mathrm{P}$ が動きうる範囲 $V$ の体積を求めよ。

　(i) $\mathrm{OP}\leqq \sqrt{3}$
　(ii) 線分 $\mathrm{OP}$ と $S$ は、共有点を持たないか、点 $\mathrm{P}$ のみを共有点に持つ。

解答

点 $\mathrm{A}$ が条件(i), (ii) を満たすとき、点 $\mathrm{P}$ は点 $\mathrm{A}$ に到達可能である、ということにする。

原点を中心する半径 $\sqrt{3}$ の球（内部及び表面）を球 $\mathrm{O}$ とおく。

以下、点 $\mathrm{Q}$ は、立方体の表面上を動くものとする。

(a) 点 $\mathrm{Q}$ が $S$ 上、または、平面 $z=1$ 内にある立方体の辺上にあるとき

線分 $\mathrm{OQ}$ の長さは、 $\sqrt{1^2+1^2+1^2}=\sqrt{3}$ 以下である。このことと、 $\mathrm{Q}$ の取り方から、線分 $\mathrm{OQ}$ 上の点には到達可能であることがわかる。

このとき、線分 $\mathrm{OQ}$ の動きうる範囲の体積は、底面積が $4$ で高さが $1$ の四面体5つ分の体積なので、\[ \frac{1}{3}\cdot 4\cdot 1 \cdot 5=\frac{20}{3} \]である。なお、条件(ii)から、線分 $\mathrm{OQ}$ の $\mathrm{Q}$ 側の延長線上には、到達可能でないことがわかる。

(b) 点 $\mathrm{Q}$ が(a)以外の場所にあるとき（平面 $z=1$ 内にある立方体の表面のうち、辺を除いた部分）

半直線 $\mathrm{OQ}$ と球 $\mathrm{O}$ との交点を $\mathrm{R}$ とおく。線分 $\mathrm{OR}$ は $S$ と共有点を持たないことから、線分 $\mathrm{OR}$ 上の点には到達可能であることがわかる。

$\mathrm{Q}$ が立方体のほかの表面にいる場合に同様のことを考えると、線分 $\mathrm{OR}$ の動きうる範囲は、対称性から、球 $\mathrm{O}$ を6分割したものであることがわかる。よって、この場合に動きうる範囲の体積は\[ \frac{1}{6} \cdot \dfrac{4}{3}\pi(\sqrt{3})^3=\frac{2\sqrt{3}}{3}\pi \]である。なお、条件(i)から、線分 $\mathrm{OR}$ の $\mathrm{R}$ 側の延長線上には、到達可能でないことがわかる。

(a)(b)以外に到達可能な点はなく、(a)(b)に重複はないので、$V$ の体積は\[ \frac{20+2\sqrt{3}\pi}{3} \]となる。（答）

解答編　つづき

問題

(2) 座標空間内の点 $\mathrm{N}$ と点 $\mathrm{P}$ が次の条件(iii), (iv), (v) をすべて満たすとき、点 $\mathrm{P}$ が動きうる範囲 $W$ の体積を求めよ。必要ならば、 $\sin\alpha=\dfrac{1}{\sqrt{3}}$ を満たす実数 $\alpha$ $\left(0\lt \alpha\lt\dfrac{\pi}{2} \right)$ を用いてよい。

　(iii) $\mathrm{ON+NP}\leqq \sqrt{3}$
　(iv) 線分 $\mathrm{ON}$ と $S$ は共有点を持たない。
　(v) 線分 $\mathrm{NP}$ と $S$ は、共有点を持たないか、点 $\mathrm{P}$ のみを共有点に持つ。

解答

$\mathrm{N}$ が $\mathrm{O}$ にあるときを考えると、条件(iii)(iv)(v) は条件(i)(ii) と同値になるので、 $W$ は $V$ を含むことがわかる。以下では、 $W$ のうち、 $V$ を含まない部分を考えることにする。条件(iii)を満たすとき、条件(i)が成り立つことから、条件(iii)(iv)(v) を満たすが条件(ii) を満たさない場合を考えればよい。

点 $\mathrm{P}$ は、 $W$ のうち $V$ を含まない部分にあるとする。条件(ii) を満たさないので、線分 $\mathrm{OP}$ は、$S$ と共有点をもち、この共有点は、点 $\mathrm{P}$ 以外である。この共有点を $\mathrm{Q}$ とおく。

(a) 点 $\mathrm{Q}$ が平面 $x=1$ 上にある立方体の表面上にある場合

点 $\mathrm{A}(1,-1,1)$, $\mathrm{B}(1,1,1)$ とおき、3点 $\mathrm{O,A,B}$ で定まる平面を、平面 $\alpha$ とおく。

点 $\mathrm{P}$ が平面 $y=t$ にあるとして、この平面で切ったときの断面を考える。

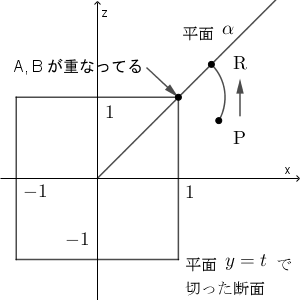
$\mathrm{AB}$ を軸として点 $\mathrm{P}$ を回転させ、平面 $\alpha$ 上にくるように移動させる（立方体と共有点を持たない方向に回転させる）。このときの移動後の点を $\mathrm{R}$ とすると、 $\mathrm{OR}\leqq \sqrt{3}$ であることと、 $\mathrm{P}$ が条件(iii)(iv)(v) を満たすことは同値である。（ $\mathrm{N}$ として、線分 $\mathrm{OQ_2}$ と立方体の $z=1$ 上にある辺との共有点をとるときに $\mathrm{ON+NP}=\mathrm{ON+NR}$ の値が最小となるため）

よって、球 $\mathrm{O}$ を平面 $\alpha$ で切ったときの断面のうち、三角形 $\mathrm{OAB}$ を取り除いた部分（つまり、弧 $\mathrm{AB}$ と線分 $\mathrm{AB}$ で囲まれた部分）を、直線 $\mathrm{AB}$ を軸に $\dfrac{3}{4}\pi$ だけ $z$ 軸の負の方向に回転したときに通過する領域が、 $\mathrm{P}$ の到達可能な範囲である。

この領域を平面 $y=t$ で切断したとき、平面 $\alpha$ 上では次のようになる。（赤線の部分）

よって、断面の面積は、半径 $\sqrt{3-t^2}-\sqrt{2}$ で中心角が $\dfrac{3}{4}\pi$ のおうぎ形なので
\begin{eqnarray} & & \int_{-1}^1 \frac{1}{2}(\sqrt{3-t^2}-\sqrt{2})^2 \cdot\frac{3}{4}\pi dt \\[5pt] &=& \frac{3}{8}\pi \int_{-1}^1 (5-t^2-2\sqrt{2}\sqrt{3-t^2}) dt \\[5pt] \end{eqnarray}となる。ここで、 \begin{eqnarray} & & \frac{3}{8}\pi \int_{-1}^1 (5-t^2) dt \\[5pt] &=& \frac{3}{8}\pi \cdot 2\cdot \left[5t-\frac{t^3}{3}\right]_0^1 \\[5pt] &=& \frac{3}{4}\pi \left(5-\frac{1}{3}\right) \\[5pt] &=& \frac{3}{4}\pi \cdot \frac{14}{3} \\[5pt] &=& \frac{7}{2}\pi \\[5pt] \end{eqnarray} であり、
\begin{eqnarray} & & \frac{3}{8}\pi \int_{-1}^1 (-2\sqrt{2}\sqrt{3-t^2}) dt \\[5pt] &=& -\frac{3\sqrt{2}}{4}\pi \int_{-1}^1 (\sqrt{3-t^2}) dt \\[5pt] \end{eqnarray}となる。このうち、積分の部分は、次の図の斜線部分の面積である。

よって、
\begin{eqnarray} & & -\frac{3\sqrt{2}}{4}\pi \int_{-1}^1 (\sqrt{3-t^2}) dt \\[5pt] &=& -\frac{3\sqrt{2}}{4}\pi \cdot 2\cdot \left(\frac{3\alpha}{2}+\frac{\sqrt{2}}{2}\right) \\[5pt] &=& -\frac{3\sqrt{2}}{4}\pi (3\alpha+\sqrt{2}) \\[5pt] &=& -\frac{9\sqrt{2}\alpha}{4}\pi -\frac{3}{2}\pi \end{eqnarray}となるので、 \begin{eqnarray} & & \frac{7}{2}\pi-\frac{9\sqrt{2}\alpha}{4}\pi -\frac{3}{2}\pi \\[5pt] &=& 2\pi-\frac{9\sqrt{2}\alpha}{4}\pi \\[5pt] \end{eqnarray}となる。

(b) 点 $\mathrm{Q}$ が平面 $x=-1$, $y=1$, $y=-1$ 上にある立方体の表面上にある場合

それぞれ、(a)のときと同じであり、これらに共有部分はない。

(c) 点 $\mathrm{Q}$ が平面 $z=-1$ 上にある立方体の表面上にある場合

(a)で見た内容より、この場合は条件(iii)を満たすことはない。

(a)(b)(c)から、$V$ の体積に、(a)で得られた結果を4倍して足したものが $W$ の体積なので
\begin{eqnarray} & & \frac{20+2\sqrt{3}\pi}{3}+4\left( 2\pi-\frac{9\sqrt{2}\alpha}{4}\pi \right) \\[5pt] &=& \frac{20+2\sqrt{3}\pi}{3}+8\pi-9\sqrt{2}\alpha\pi \\[5pt] \end{eqnarray} …（答）