東京大学 理系 2006年度後期 第2問 解説
問題編
【問題】
aを正の実数、$\theta$を$\displaystyle 0\leqq \theta \leqq \frac{\pi}{2}$を満たす実数とする。xyz空間において、点$(a,0,0)$と点$(a+\cos \theta,0,\sin\theta)$を結ぶ線分を、x軸のまわりに1回転させてできる曲面をSとする。さらに、Sをy軸のまわりに1回転させてできる立体の体積をVとする。
次の問に答えよ。(1) Vをaと$\theta$を用いて表せ。
(2) $a=4$とする。Vを$\theta$の関数と考えて、Vの最大値を求めよ。
【考え方】
2回も回転するので面倒ですが、基本的には「平面$y=t$で切った断面積を積分する」という方針でいきます。Sを平面$y=t$で切った断面の形は気にする必要はなく、y軸から一番近い点と遠い点さえわかればOKです。あとはドーナツ型の断面を使って、積分すれば(1)は出ます。
(1)が求められれば、(2)はおまけみたいな問題です。
解答編
【問題】
aを正の実数、$\theta$を$\displaystyle 0\leqq \theta \leqq \frac{\pi}{2}$を満たす実数とする。xyz空間において、点$(a,0,0)$と点$(a+\cos \theta,0,\sin\theta)$を結ぶ線分を、x軸のまわりに1回転させてできる曲面をSとする。さらに、Sをy軸のまわりに1回転させてできる立体の体積をVとする。
次の問に答えよ。(1) Vをaと$\theta$を用いて表せ。
【解答】
$\mathrm{ A }(a,0,0)$、$\mathrm{ B }(a+\cos\theta,0,\sin\theta)$とする。
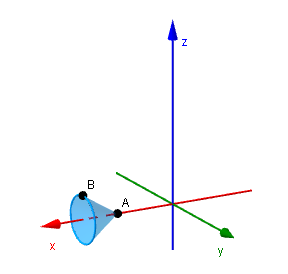
線分AB上の点Cは実数$s\ (0\leqq s\leqq 1)$を用いて、\[ (a+s\cos\theta,0,s\sin\theta) \]と書ける。点Cを、x軸を中心に回転すると、平面$x=a+s\cos\theta$内に、点$(a+s\cos\theta,0,0)$を中心とした半径$s\sin\theta$の円ができあがる。よって、S上の点は、$\alpha \ (0\leqq \alpha\lt 2\pi)$を用いて\[ (a+s\cos\theta,s \sin\theta \cos\alpha, s \sin\theta \sin\alpha) \]と書ける。
$-\sin\theta \leqq s \sin\theta \cos\alpha \leqq \sin\theta$なので、平面$y=t$と曲面Sが共有点を持つとすると、$t=s \sin\theta \cos\alpha$より、$-\sin\theta \leqq t \leqq \sin\theta$となる。tがこの範囲のとき、平面$y=t$と曲面Sとの共有点とy軸との距離の2乗は、
\begin{eqnarray}
& &
(a+s\cos\theta)^2+(s \sin\theta \sin\alpha)^2 \\
&=&
a^2 +2as\cos\theta +s^2\cos^2\theta \\
& & +s^2 \sin^2\theta \sin^2\alpha \\[5pt]
&=&
a^2 +2as\cos\theta +s^2\cos^2\theta \\
& & +s^2 \sin^2\theta (1-\cos^2\alpha) \\[5pt]
&=&
a^2 +2as\cos\theta +s^2 -t^2 \\
\end{eqnarray}となる。$-a\cos\theta \leqq 0$なので、$0\leqq s \leqq 1$の範囲で単調増加である。
$t\ne 0$とする。$\displaystyle t=s \sin\theta \cos\alpha$なので、$\displaystyle s=\frac{t}{\sin\theta \cos\alpha}$であり、$\alpha$は$0\leqq \alpha\lt 2\pi$の範囲を自由に動けるので、$\displaystyle \frac{|t|}{\sin\theta} \leqq s \leqq 1$となる。よって、平面$y=t$と曲面Sとの共有点のうち、y軸との距離が最小になるのは、$\displaystyle s=\frac{|t|}{\sin\theta}$のときであり、最大となるのは$s=1$のときとなる。これは、$t=0$のときも成り立つ。
以上から、Sをy軸を中心に1回転してできる立体を、平面$y=t$で切断すると、その断面積は
\begin{eqnarray}
& &
\pi \left\{ \left( a^2 +2a\cos\theta +1 -t^2 \right) -\left( a^2 +2a\frac{|t|}{\sin\theta}\cos\theta +\frac{|t|^2}{\sin^2\theta} -t^2 \right) \right\} \\[5pt]
&=&
\pi \left( 2a\cos\theta +1 -2a\frac{|t|\cos\theta}{\sin\theta} -\frac{t^2}{\sin^2\theta} \right) \\[5pt]
\end{eqnarray}となる。$-\sin\theta \leqq t \leqq \sin\theta$だから、求める体積Vは
\begin{eqnarray}
V
&=&
\int_{-\sin\theta}^{\sin\theta} \pi \left( 2a\cos\theta +1 -2a\frac{|t|\cos\theta}{\sin\theta} -\frac{t^2}{\sin^2\theta} \right) dt \\[5pt]
&=&
2\pi \int_0^{\sin\theta} \left( 2a\cos\theta +1 -2a\frac{t\cos\theta}{\sin\theta} -\frac{t^2}{\sin^2\theta} \right) dt \\[5pt]
&=&
2\pi \left[(2a\cos\theta +1)t -a\frac{t^2\cos\theta}{\sin\theta} -\frac{t^3}{3\sin^2\theta} \right]_0^{\sin\theta} \\[5pt]
&=&
2\pi \left\{(2a\cos\theta +1)\sin\theta -a\frac{\sin^2\theta\cos\theta}{\sin\theta} -\frac{\sin^3\theta}{3\sin^2\theta} \right\} \\[5pt]
&=&
2\pi \left\{ (2a\cos\theta +1)\sin\theta -a\sin\theta\cos\theta -\frac{\sin\theta}{3} \right\} \\[5pt]
&=&
2\pi \sin\theta \left( a\cos\theta +\frac{2}{3} \right) \\[5pt]
\end{eqnarray}となる。
【解答終】
【解説】
ここでは、図形的に考えることなく、最後まで計算だけで解いています。図形的に考えると、もう少し楽ができる部分はあります。
平面$y=t$でSを切ったとき、断面上の点とy軸との距離を考えた場合、図を描けば、最小になるのは$z=0$のとき、最大になるのは$x=a+\cos\theta$のときであることはすぐにわかります。このことを使えば、もう少し楽をすることはできます。
【問題】
(2) $a=4$とする。Vを$\theta$の関数と考えて、Vの最大値を求めよ。
【解答】
(1)より、$a=4$とすると、
\begin{eqnarray}
V
&=&
2\pi \sin\theta \left( 4\cos\theta +\frac{2}{3} \right) \\[5pt]
&=&
8\pi \sin\theta \cos\theta +\frac{4\pi\sin\theta}{3} \\[5pt]
\end{eqnarray}となる。これを$\theta$で微分すると
\begin{eqnarray}
& &
8\pi (\cos^2\theta -\sin^2\theta) +\frac{4\pi\cos\theta}{3} \\[5pt]
&=&
8\pi (2\cos^2\theta -1) +\frac{4\pi\cos\theta}{3} \\[5pt]
&=&
\frac{4\pi}{3} (12\cos^2\theta +\cos\theta -6) \\[5pt]
&=&
\frac{4\pi}{3} (3\cos\theta -2)(4\cos\theta +3) \\[5pt]
\end{eqnarray}となる。$\cos\theta_1=\frac{2}{3}$を満たす$\theta_1 \ (0\leqq \theta_1\leqq\frac{\pi}{2})$がただ1つ存在するので、増減表は次のようになる。
\begin{array}{c|ccccc}
\theta & 0 & \cdots & \theta_1 & \cdots & \frac{\pi}{2} \\
\hline
V' & & + & 0 & - & \\
\hline
V & & \nearrow & & \searrow &
\end{array}
$\sin\theta_1=\frac{\sqrt{5} }{3}$なので、求める最大値は
\begin{eqnarray}
V
&=&
2\pi \cdot \frac{\sqrt{5} }{3} \left( 4\cdot \frac{2}{3} +\frac{2}{3} \right) \\[5pt]
&=&
2\pi \cdot \frac{\sqrt{5} }{3} \cdot \frac{10}{3} \\[5pt]
&=&
\frac{20\sqrt{5} }{9}\pi \\[5pt]
\end{eqnarray}となる。
【解答終】
【解説】
(1)ができれば、微分して増減表を書くだけです。





