東京大学 文系 2016年度 第1問 解説
問題編
【問題】
座標平面上の3点$\mathrm{ P }(x,y)$、$\mathrm{ Q }(-x,-y)$、$\mathrm{ R }(1,0)$が鋭角三角形をなすための$(x,y)$についての条件を求めよ。また、その条件をみたす点Pの範囲を図示せよ。
【考え方】
いろいろやり方はあると思いますが、ここではベクトルの内積を使ってみます。内積が正になる条件を考える、というやりかたで攻めてみます。
解答編
【問題】
座標平面上の3点$\mathrm{ P }(x,y)$、$\mathrm{ Q }(-x,-y)$、$\mathrm{ R }(1,0)$が鋭角三角形をなすための$(x,y)$についての条件を求めよ。また、その条件をみたす点Pの範囲を図示せよ。
【解答】
PQRが三角形となるには、$(x,y)\ne (1,0)$と$(x,y)\ne (-1,0)$が必要。また、PQ上にRが来ることはない。
$\overrightarrow{ \mathrm{ PQ } } \cdot \overrightarrow{ \mathrm{ PR } } = |\overrightarrow{ \mathrm{ PQ } }||\overrightarrow{ \mathrm{ PR } }|\cos \angle \mathrm{ QPR }$なので、$\angle \mathrm{ QPR }$が鋭角であることと、この内積が正であることは同値。
よって
\begin{eqnarray}
\overrightarrow{ \mathrm{ PQ } } \cdot \overrightarrow{ \mathrm{ PR } } & \gt & 0 \\
(-2x)(1-x) + (-2y)(-y) & \gt & 0 \\
x^2-x + y^2 & \gt & 0 \\
\left(x-\frac{1}{2}\right)^2 + y^2 & \gt & \frac{1}{4}
\end{eqnarray}を満たせばよい。
同様に、
\begin{eqnarray}
\overrightarrow{ \mathrm{ QP } } \cdot \overrightarrow{ \mathrm{ QR } } & \gt & 0 \\
2x(1+x) + 2y\cdot y & \gt & 0 \\
x^2+x + y^2 & \gt & 0 \\
\left(x+\frac{1}{2}\right)^2 + y^2 & \gt & \frac{1}{4}
\end{eqnarray}と
\begin{eqnarray}
\overrightarrow{ \mathrm{ RP } } \cdot \overrightarrow{ \mathrm{ RQ } } & \gt & 0 \\
(x-1)(-x-1) + y(-y) & \gt & 0 \\
x^2-1 + y^2 & \lt & 0 \\
x^2 + y^2 & \lt & 1
\end{eqnarray}も満たせば、それぞれの角は鋭角となる。
以上から、求める条件は次の通り(すべてを同時に満たすもの)。
\begin{eqnarray}
\left(x-\frac{1}{2}\right)^2 + y^2 & \gt & \frac{1}{4} \\[5pt]
\left(x+\frac{1}{2}\right)^2 + y^2 & \gt & \frac{1}{4} \\[5pt]
x^2 + y^2 & \lt & 1
\end{eqnarray}
また、この範囲を図示すると、次の図の灰色の部分となる。ただし、境界線は含まない。
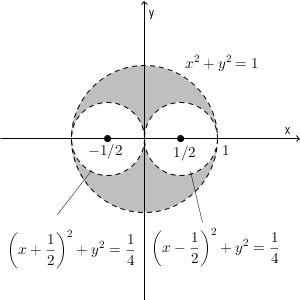
【解答終】
【解説】
内積を使わなくても、$\mathrm{ PQ }^2+\mathrm{ QR }^2 \gt \mathrm{ PR }^2$などの式から計算してもいいですね。そんなに計算するところもなく、ひっかけもありません。やさしめな1問目なので、ぜひとっておきたいところです。





