東京大学 文系 2006年度 第1問 解説
問題編
【問題】
四角形ABCDが、半径$\displaystyle \frac{65}{8}$の円に内接している。この四角形の周の長さが$44$で、辺BCと辺CDの長さがいずれも$13$であるとき、残りの2辺ABとDAの長さを求めよ。
【考え方】
使える条件が少ないように見えますが、円に内接している三角形がたくさんあるので、実は使える条件はたくさんあります。余弦定理も組み合わせれば、いろいろな辺と角を求めることができます。三角比の公式を使いこなせないといけない上、計算が少し煩雑です。
ここでは、ACに着目して解いていきます。
解答編
【問題】
四角形ABCDが、半径$\displaystyle \frac{65}{8}$の円に内接している。この四角形の周の長さが$44$で、辺BCと辺CDの長さがいずれも$13$であるとき、残りの2辺ABとDAの長さを求めよ。
【解答】
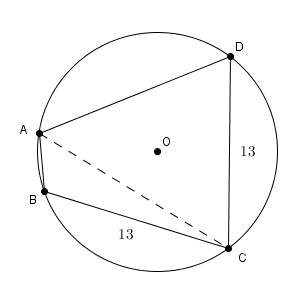
ABの長さを$x$とする。ADの長さは$18-x$となる。
三角形ABCに対して余弦定理を用いると、
\begin{eqnarray}
\mathrm{ AC }^2
&=&
\mathrm{ AB }^2+\mathrm{ BC }^2-2 \cdot \mathrm{ AB } \cdot \mathrm{ BC } \cos\angle\mathrm{ ABC } \\
&=&
x^2+13^2-26x \cos\angle\mathrm{ ABC }
\end{eqnarray}となる。
また、三角形ADCに対して余弦定理を用いると
\begin{eqnarray}
\mathrm{ AC }^2
&=&
\mathrm{ AD }^2+\mathrm{ CD }^2-2 \cdot \mathrm{ AD } \cdot \mathrm{ CD } \cos\angle\mathrm{ ADC } \\
&=&
(18-x)^2+13^2-26(18-x) \cos\angle\mathrm{ ADC } \\
\end{eqnarray}となる。
よって、
\begin{eqnarray}
x^2+13^2-26x \cos\angle\mathrm{ ABC }
&=&
(18-x)^2+13^2 -26(18-x) \cos\angle\mathrm{ ADC }
\\
-26x \cos\angle\mathrm{ ABC }
&=&
-36x+18^2 +26(18-x) \cos\angle\mathrm{ ABC }
\\
-26\cdot 18 \cdot \cos\angle\mathrm{ ABC }
&=&
-36x+18^2
\\[5pt]
\cos\angle\mathrm{ ABC }
&=&
\frac{-36x+18^2}{-26\cdot 18} \\[5pt]
&=&
\frac{x-9}{13} \quad \cdots (a)
\\
\end{eqnarray}となる。
また、正弦定理より
\begin{eqnarray}
2\cdot\frac{65}{8} \sin\angle\mathrm{ ABC } &=& \mathrm{ AC } \\
\end{eqnarray}なので、両辺を2乗して(a)を代入すると
\begin{eqnarray}
\frac{65^2}{4^2} \sin^2 \angle\mathrm{ ABC } &=& x^2+13^2-26x \cos\angle\mathrm{ ABC } \\[5pt]
\frac{65^2}{4^2} \cdot \frac{13^2-(x-9)^2}{13^2} &=& x^2+13^2-26x \cdot \frac{x-9}{13} \\[5pt]
\frac{25(-x^2+18x+88)}{4^2} &=& x^2+13^2-2x(x-9) \\[5pt]
\end{eqnarray}となる。さらに変形して
\begin{eqnarray}
25(-x^2+18x+88) &=& 16(-x^2+18x+13^2) \\[5pt]
-9x^2+18(25-16)x+8(25\cdot 11-2\cdot 13^2) &=& 0 \\[5pt]
-9x^2+18\cdot 9x-8\cdot 63 &=& 0 \\[5pt]
x^2-18x+56 &=& 0 \\[5pt]
(x-4)(x-14) &=& 0 \\[5pt]
\end{eqnarray}となる。
$x=4,14$のとき、それぞれ$\mathrm{ AD }=14,4$となるから、ABとDAの長さは、4と14、または、14と4となる。
【解答終】
【解説】
上の解答では、ACに着目して解いていきました。しかし、BDに着目して解くという方法もあります。三角形BCDについて、余弦定理と正弦定理を組み合わせれば、BDを直接求めることができます。さらに三角形ABDに対して余弦定理を使えば、答えを求めることができます。





