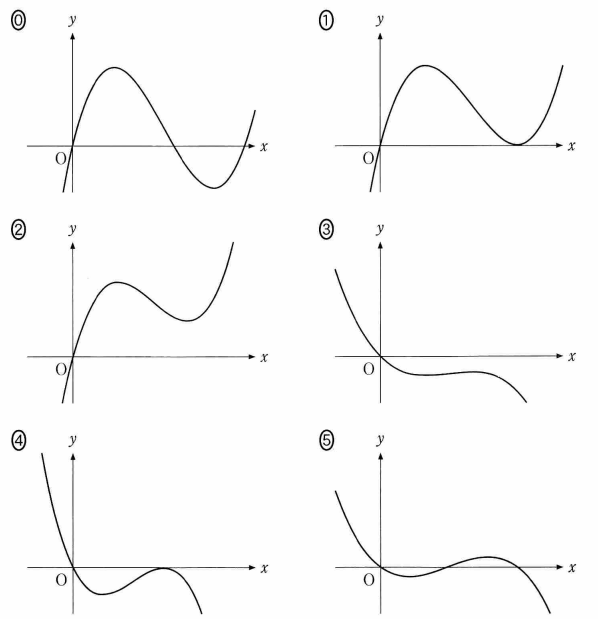
共通テスト 数学II・数学B 2024年度 第2問 解説
【必答問題】
問題編
問題
$m$ を $m\gt 1$ を満たす定数とし、 $f(x)=3(x-1)(x-m)$ とする。また、 $\displaystyle S(x)=\int_0^x f(t)dt$ とする。関数 $y=f(x)$ と $y=S(x)$ のグラフの関係について考えてみよう。
(1) $m=2$ のとき、すなわち、 $f(x)=3(x-1)(x-2)$ のときを考える。
(i) $f'(x)=0$ となる $x$ の値は $x=\dfrac{\myBox{ア}}{\myBox{イ}}$ である。
(ii) $S(x)$ を計算すると
\begin{eqnarray} S(x) &=& \int_0^x f(t) dt \\[5pt] &=& \int_0^x\left(3t^2-\myBox{ウ}t+\myBox{エ}\right) dt \\[5pt] &=& x^3-\frac{\myBox{オ}}{\myBox{カ}}x^2+\myBox{キ}x \end{eqnarray}であるから$x=\myBox{ク}$ のとき、 $S(x)$ は極大値 $\dfrac{\myBox{ケ}}{\myBox{コ}}$ をとり
$x=\myBox{サ}$ のとき、 $S(x)$ は極小値 $\myBox{シ}$ をとることがわかる。
(iii) $f(3)$ と一致するものとして、次の 0 ~ 4 のうち、正しいものは $\dBox{ス}$ である。
$\dbox{ス}$ の解答群
0: $S(3)$
1: 2点 $(2,S(2)), (4,S(4))$ を通る直線の傾き
2: 2点 $(0,0),(3,S(3))$ を通る直線の傾き
3: 関数 $y=S(x)$ のグラフ上の点 $(3,S(3))$ における接線の傾き
4: 関数 $y=f(x)$ のグラフ上の点 $(3,f(3))$ における接線の傾き(2) $0\leqq x\leqq 1$ の範囲で、関数 $y=f(x)$ のグラフと $x$ 軸および $y$ 軸で囲まれた図形の面積を $S_1$、 $1\leqq x\leqq m$ の範囲で、関数 $y=f(x)$ のグラフと $x$ 軸で囲まれた図形の面積を $S_2$ とする。このとき、 $S_1=\dBox{セ}$, $S_2=\dBox{ソ}$ である。
$S_1=S_2$ となるのは $\dBox{タ}=0$ のときであるから、 $S_1=S_2$ が成り立つような $f(x)$ に対する関数 $y=S(x)$ のグラフの概形は $\dBox{チ}$ である。また、 $S_1\gt S_2$ が成り立つような $f(x)$ に対する関数 $y=S(x)$ のグラフの概形は $\dBox{ツ}$ である。
$\dbox{セ}$, $\dbox{ソ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\int_0^1 f(x)dx$
1: $\int_0^m f(x)dx$
2: $\int_1^m f(x)dx$
3: $\int_0^1 \{-f(x)\}dx$
4: $\int_0^m \{-f(x)\}dx$
5: $\int_1^m \{-f(x)\}dx$
$\dbox{タ}$ の解答群
0: $\int_0^1 f(x)dx$
1: $\int_0^m f(x)dx$
2: $\int_1^m f(x)dx$
3: $\int_0^1 f(x)dx-\int_0^m f(x)dx$
4: $\int_0^1 f(x)dx-\int_1^m f(x)dx$
5: $\int_0^1 f(x)dx+\int_0^m f(x)dx$
6: $\int_0^m f(x)dx+\int_1^m f(x)dx$
$\dbox{チ}$, $\dbox{ツ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
(3) 関数 $y=f(x)$ のグラフの特徴から関数 $y=S(x)$ のグラフの特徴を考えてみよう。
関数 $y=f(x)$ のグラフは直線 $x=\dBox{テ}$ に関して対称であるから、すべての正の実数 $p$ に対して\[ \int_{1-p}^1 f(x)dx = \int_m^{\dBox{ト}} f(x)dx \quad\cdots ① \]が成り立ち、 $M=\dbox{テ}$ とおくと $0\lt q\leqq M-1$ であるすべての実数 $q$ に対して\[ \int_{M-q}^M \{-f(x)\}dx = \int_M^{\dBox{ナ}} \{-f(x)\}dx \quad \cdots ② \]が成り立つことがわかる。すべての実数 $\alpha,\beta$ に対して\[ \int_{\alpha}^{\beta}f(x)dx=S(\beta)-S(\alpha) \]が成り立つことに注意すれば、①と②はそれぞれ
\begin{eqnarray} & & S(1-p)+S\left(\dbox{ト}\right)=\dBox{ニ} \\[5pt] & & 2S(M)=\dBox{ヌ} \end{eqnarray}となる。以上から、すべての正の実数 $p$ に対して、2点 $(1-p,S(1-p))$, $\left(\dbox{ト},S\left(\dbox{ト}\right)\right)$ を結ぶ線分の中点についての記述として、後の 0 ~ 5 のうち、最も適当なものは $\dBox{ネ}$ である。
$\dbox{テ}$ の解答群
0: $m$
1: $\dfrac{m}{2}$
2: $m+1$
3: $\dfrac{m+1}{2}$
$\dbox{ト}$ の解答群
0: $1-p$
1: $p$
2: $1+p$
3: $m-p$
4: $m+p$$\dbox{ナ}$ の解答群
0: $M-q$
1: $M$
2: $M+q$
3: $M+m-q$
4: $M+m$
5: $M+m+q$$\dbox{ニ}$ の解答群
0: $S(1)+S(m)$
1: $S(1)+S(p)$
2: $S(1)-S(m)$
3: $S(1)-S(p)$
4: $S(p)-S(m)$
5: $S(m)-S(p)$$\dbox{ヌ}$ の解答群
0: $S(M-q)+S(M+m-q)$
1: $S(M-q)+S(M+m)$
2: $S(M-q)+S(M)$
3: $2S(M-q)$
4: $S(M+q)+S(M-q)$
5: $S(M+m+q)+S(M-q)$$\dbox{ネ}$ の解答群
0: $x$ 座標は $p$ の値によらず一つに定まり、 $y$ 座標は $p$ の値により変わる。
1: $x$ 座標は $p$ の値により変わり、 $y$ 座標は $p$ の値によらず一つに定まる。
2: 中点は $p$ の値によらず一つに定まり、関数 $y=S(x)$ のグラフ上にある。
3: 中点は $p$ の値によらず一つに定まり、関数 $y=f(x)$ のグラフ上にある。
4: 中点は $p$ の値によって動くが、つねに関数 $y=S(x)$ のグラフ上にある。
5: 中点は $p$ の値によって動くが、つねに関数 $y=f(x)$ のグラフ上にある。
考え方
単純に積分を計算できるだけでは解ききるのは難しいです。面積との関係を理解していないと途中で行き詰ってしまうでしょう。
最後は文字が多く抽象的なので、計算だけで進まずに、図形をかきながら考えるとわかりやすいでしょう。なお、 $q$ にどんな値を入れればいいかは自分で考えないといけません。
【必答問題】
解答編
問題
$m$ を $m\gt 1$ を満たす定数とし、 $f(x)=3(x-1)(x-m)$ とする。また、 $\displaystyle S(x)=\int_0^x f(t)dt$ とする。関数 $y=f(x)$ と $y=S(x)$ のグラフの関係について考えてみよう。
(1) $m=2$ のとき、すなわち、 $f(x)=3(x-1)(x-2)$ のときを考える。
(i) $f'(x)=0$ となる $x$ の値は $x=\dfrac{\myBox{ア}}{\myBox{イ}}$ である。
解説
(1)
(i)
\begin{eqnarray}
f(x)
&=&
3(x-1)(x-2) \\[5pt]
&=&
3(x^2-3x+2) \\[5pt]
&=&
3x^2-9x+6 \\[5pt]
\end{eqnarray}なので、 $f'(x)=6x-9$ だから、 $f'(x)=0$ となる $x$ の値は $x=\dfrac{3}{2}$ です。
解答
アイ:32 (2点)
解答編 つづき
問題
(ii) $S(x)$ を計算すると
\begin{eqnarray} S(x) &=& \int_0^x f(t) dt \\[5pt] &=& \int_0^x\left(3t^2-\myBox{ウ}t+\myBox{エ}\right) dt \\[5pt] &=& x^3-\frac{\myBox{オ}}{\myBox{カ}}x^2+\myBox{キ}x \end{eqnarray}であるから$x=\myBox{ク}$ のとき、 $S(x)$ は極大値 $\dfrac{\myBox{ケ}}{\myBox{コ}}$ をとり
$x=\myBox{サ}$ のとき、 $S(x)$ は極小値 $\myBox{シ}$ をとることがわかる。
解説
(ii)
\begin{eqnarray}
S(x)
&=&
\int_0^x f(t) dt \\[5pt]
&=&
\int_0^x (3t^2-9t+6) dt \\[5pt]
&=&
\left[t^3-\frac{9}{2}t^2+6t \right]_0^x \\[5pt]
&=&
x^3-\frac{9}{2}x^2+6x \\[5pt]
\end{eqnarray}となります。
一般に、 $S'(x)=f(x)$ となります(微分積分学の基本定理といいます。参考:【基本】定積分と微分の関係)。よって、 $S'(x)=f(x)=3(x-1)(x-2)$ となります。これより、増減表は次のようになります。
\begin{array}{c|ccccc}
x & \cdots & 1 & \cdots & 2 & \cdots \\
\hline
S'(x) & + & 0 & - & 0 & + \\
\hline
S(x) & \nearrow & & \searrow & & \nearrow &
\end{array}
これより、 $S(x)$ は $x=1$ のときに極大値\[ S(1)=1-\frac{9}{2}+6 = \frac{5}{2} \]をとり、 $x=2$ のときに極小値\[ S(2)=8-\frac{9}{2}\cdot4+12=2 \]をとることがわかります。
解答
ウエ:96 (1点)
オカキ:926 (2点)
ク:1 (1点)
ケコ:52 (1点)
サ:2 (1点)
シ:2 (1点)
解答編 つづき
問題
(iii) $f(3)$ と一致するものとして、次の 0 ~ 4 のうち、正しいものは $\dBox{ス}$ である。
$\dbox{ス}$ の解答群
0: $S(3)$
1: 2点 $(2,S(2)), (4,S(4))$ を通る直線の傾き
2: 2点 $(0,0),(3,S(3))$ を通る直線の傾き
3: 関数 $y=S(x)$ のグラフ上の点 $(3,S(3))$ における接線の傾き
4: 関数 $y=f(x)$ のグラフ上の点 $(3,f(3))$ における接線の傾き
解説
(iii)
$S'(x)=f(x)$ なので、 $f(3)$ は $y=S(x)$ のグラフ上の点 $(3,S(3))$ における接線の傾きと一致します。
解答
ス:3 (3点)
解答編 つづき
問題
(2) $0\leqq x\leqq 1$ の範囲で、関数 $y=f(x)$ のグラフと $x$ 軸および $y$ 軸で囲まれた図形の面積を $S_1$、 $1\leqq x\leqq m$ の範囲で、関数 $y=f(x)$ のグラフと $x$ 軸で囲まれた図形の面積を $S_2$ とする。このとき、 $S_1=\dBox{セ}$, $S_2=\dBox{ソ}$ である。
$S_1=S_2$ となるのは $\dBox{タ}=0$ のときであるから、 $S_1=S_2$ が成り立つような $f(x)$ に対する関数 $y=S(x)$ のグラフの概形は $\dBox{チ}$ である。また、 $S_1\gt S_2$ が成り立つような $f(x)$ に対する関数 $y=S(x)$ のグラフの概形は $\dBox{ツ}$ である。
$\dbox{セ}$, $\dbox{ソ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\int_0^1 f(x)dx$
1: $\int_0^m f(x)dx$
2: $\int_1^m f(x)dx$
3: $\int_0^1 \{-f(x)\}dx$
4: $\int_0^m \{-f(x)\}dx$
5: $\int_1^m \{-f(x)\}dx$
$\dbox{タ}$ の解答群
0: $\int_0^1 f(x)dx$
1: $\int_0^m f(x)dx$
2: $\int_1^m f(x)dx$
3: $\int_0^1 f(x)dx-\int_0^m f(x)dx$
4: $\int_0^1 f(x)dx-\int_1^m f(x)dx$
5: $\int_0^1 f(x)dx+\int_0^m f(x)dx$
6: $\int_0^m f(x)dx+\int_1^m f(x)dx$
$\dbox{チ}$, $\dbox{ツ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
解説
(2)
$m\gt 1$ なので、 $y=f(x)=3(x-1)(x-m)$ のグラフは次のようになります。
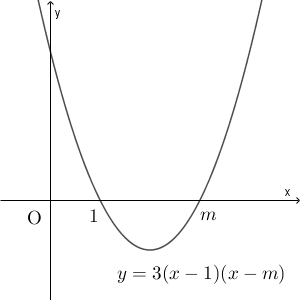
$0\lt x \lt 1$ の範囲では $f(x)\gt 0$ なので、面積 $S_1$ は\[ \int_0^1 f(x) dx \]と表すことができます。一方、 $1\lt x\lt m$ の範囲では $f(x)\lt 0$ なので、面積 $S_2$ は\[ \int_1^m \{ -f(x)\} dx \]で表すことができます。
$S_1=S_2$ となるのは
\begin{eqnarray}
\int_0^1 f(x) dx &=& \int_1^m \{ -f(x)\} dx \\[5pt]
\int_0^1 f(x) dx+\int_1^m f(x) dx &=& 0 \\[5pt]
\int_0^m f(x) dx &=& 0 \\[5pt]
\end{eqnarray}のときです。
次に、グラフについてですが、$0\lt x \lt 1$ の範囲では $f(x)\gt 0$ なので、 $S(x)$ は正です。なので、選択肢の 3, 4, 5 はすべて誤りです。
また、 $S'(x)=f(x)$ であり、 $f(x)=0$ の解が $x=1,m$ で $m\gt 1$ なので、極小値をとっているところは $x=m$ だとわかります。
$S_1=S_2$ となるのは\[ \int_0^m f(x) dx = 0 \]のときであり、これは $y=S(x)$ の極小値が $0$ ということなので、選択肢 1 が該当します。
$S_1\gt S_2$ は、先ほどと同じ式を変形すると\[ \int_0^m f(x) dx \gt 0 \]のときだとわかり、これは $y=S(x)$ の極小値が正ということなので、選択肢 2 が該当します。
解答
セソ:05 (2点)
タ:1 (2点)
チ:1 (4点)
ツ:2 (2点)
解答編 つづき
問題
(3) 関数 $y=f(x)$ のグラフの特徴から関数 $y=S(x)$ のグラフの特徴を考えてみよう。
関数 $y=f(x)$ のグラフは直線 $x=\dBox{テ}$ に関して対称であるから、すべての正の実数 $p$ に対して\[ \int_{1-p}^1 f(x)dx = \int_m^{\dBox{ト}} f(x)dx \quad\cdots ① \]が成り立ち、 $M=\dbox{テ}$ とおくと $0\lt q\leqq M-1$ であるすべての実数 $q$ に対して\[ \int_{M-q}^M \{-f(x)\}dx = \int_M^{\dBox{ナ}} \{-f(x)\}dx \quad \cdots ② \]が成り立つことがわかる。すべての実数 $\alpha,\beta$ に対して\[ \int_{\alpha}^{\beta}f(x)dx=S(\beta)-S(\alpha) \]が成り立つことに注意すれば、①と②はそれぞれ
\begin{eqnarray} & & S(1-p)+S\left(\dbox{ト}\right)=\dBox{ニ} \\[5pt] & & 2S(M)=\dBox{ヌ} \end{eqnarray}となる。以上から、すべての正の実数 $p$ に対して、2点 $(1-p,S(1-p))$, $\left(\dbox{ト},S\left(\dbox{ト}\right)\right)$ を結ぶ線分の中点についての記述として、後の 0 ~ 5 のうち、最も適当なものは $\dBox{ネ}$ である。
$\dbox{テ}$ の解答群
0: $m$
1: $\dfrac{m}{2}$
2: $m+1$
3: $\dfrac{m+1}{2}$
$\dbox{ト}$ の解答群
0: $1-p$
1: $p$
2: $1+p$
3: $m-p$
4: $m+p$$\dbox{ナ}$ の解答群
0: $M-q$
1: $M$
2: $M+q$
3: $M+m-q$
4: $M+m$
5: $M+m+q$$\dbox{ニ}$ の解答群
0: $S(1)+S(m)$
1: $S(1)+S(p)$
2: $S(1)-S(m)$
3: $S(1)-S(p)$
4: $S(p)-S(m)$
5: $S(m)-S(p)$$\dbox{ヌ}$ の解答群
0: $S(M-q)+S(M+m-q)$
1: $S(M-q)+S(M+m)$
2: $S(M-q)+S(M)$
3: $2S(M-q)$
4: $S(M+q)+S(M-q)$
5: $S(M+m+q)+S(M-q)$$\dbox{ネ}$ の解答群
0: $x$ 座標は $p$ の値によらず一つに定まり、 $y$ 座標は $p$ の値により変わる。
1: $x$ 座標は $p$ の値により変わり、 $y$ 座標は $p$ の値によらず一つに定まる。
2: 中点は $p$ の値によらず一つに定まり、関数 $y=S(x)$ のグラフ上にある。
3: 中点は $p$ の値によらず一つに定まり、関数 $y=f(x)$ のグラフ上にある。
4: 中点は $p$ の値によって動くが、つねに関数 $y=S(x)$ のグラフ上にある。
5: 中点は $p$ の値によって動くが、つねに関数 $y=f(x)$ のグラフ上にある。
解説
(3)
$y=f(x)=3(x-1)(x-m)$ なので、このグラフは直線 $x=\dfrac{m+1}{2}$ について対称です。なので、 $1-p\leqq x\leqq 1$ の部分と $m\leqq x \leqq m+p$ の部分が対応するため、\[ \int_{1-p}^1 f(x) dx =\int_m^{m+p} f(x) dx \]が成り立ちます。図形で表すと、次の赤と青の部分の面積が等しい、ということです。

また、 $M=\dfrac{m+1}{2}$ とおくと、 $M-q\leqq x\leqq M$ の部分と $M\leqq x\leqq M+q$ の部分が対応するため、\[ \int_{M-q}^M \{-f(x)\} dx =\int_M^{M+q} \{-f(x)\} dx \]が成り立ちます。図形で表すと、次の赤と青の部分の面積が等しい、ということです。

1つ目の式を変形すると
\begin{eqnarray}
\int_{1-p}^1 f(x) dx &=& \int_m^{m+p} f(x) dx \\[5pt]
S(1)-S(1-p) &=& S(m+p)-S(m) \\[5pt]
S(1)+S(m) &=& S(m+p)+S(1-p) \\[5pt]
\end{eqnarray}なので、 $S(1-p)+S(m+p)$ は $S(1)+S(m)$ と一致することがわかります。
また、2つ目の式を変形すると
\begin{eqnarray}
\int_{M-q}^M f(x) dx &=& \int_M^{M+q} f(x) dx \\[5pt]
S(M)-S(M-q) &=& S(M+q)-S(M) \\[5pt]
2S(M) &=& S(M+q)+S(M-q) \\[5pt]
\end{eqnarray}が成り立つことがわかります。
以上から、 $(1-p,S(1-p))$ と $(m+p),S(m+p)$ を結ぶ線分の中点の座標は $\left(\dfrac{m+1}{2}, \dfrac{S(1-p)+S(m+p)}{2}\right)$ となり、ニ の解答から $\left(\dfrac{m+1}{2}, \dfrac{S(m)+S(1)}{2}\right)$ と変形できることがわかります。この式には $p$ を含まないので、 $p$ の値によらずに中点が定まることがわかります。
また、ヌ の解答から\[ 2S(M) = S(M+q)+S(M-q) \]が成り立ちますが、この $M$ とは $\dfrac{m+1}{2}$ のことでした。ここで $q$ は $0\lt q\leqq M-1=\dfrac{m-1}{2}$ だったら何でもいいので、 $q=\dfrac{m-1}{2}$ としてみると
\begin{eqnarray}
2S(M) &=& S(M+q)+S(M-q) \\[5pt]
2S\left(\frac{m+1}{2}\right) &=& S\left(\frac{m+1}{2}+\frac{m-1}{2}\right)+S\left(\frac{m+1}{2}-\frac{m-1}{2}\right) \\[5pt]
2S\left(\frac{m+1}{2}\right) &=& S(m)+S(1) \\[5pt]
S\left(\frac{m+1}{2}\right) &=& \frac{S(m)+S(1)}{2} \\[5pt]
\end{eqnarray}となることがわかります。つまり、先ほどの中点の座標は\[ \left(\dfrac{m+1}{2}, \dfrac{S(m)+S(1)}{2}\right)=\left(\dfrac{m+1}{2}, S\left(\frac{m+1}{2}\right)\right) \]と書きかえることができ、中点は $y=S(x)$ 上にあることがわかります。
解答
テ:3 (1点)
トナ:42 (3点)
ニヌ:04 (2点)
ネ:2 (2点)