共通テスト 数学II・数学B 2024年度 第1問 [1] 解説

【必答問題】

問題編

問題

(1) $k\gt 0,\ k\ne 1$ とする。関数 $y=\log_k x$ と $y=\log_2 kx$ のグラフについて考えよう。

(i) $y=\log_3 x$ のグラフは点 $\left(27,\myBox{ア}\right)$ を通る。また、 $y=\log_2 \dfrac{x}{5}$ のグラフは点 $\left(\myBox{イウ},1\right)$ を通る。

(ii) $y=\log_k x$ のグラフは、 $k$ の値によらず定点 $\left(\myBox{エ},\ \myBox{オ}\right)$ を通る。

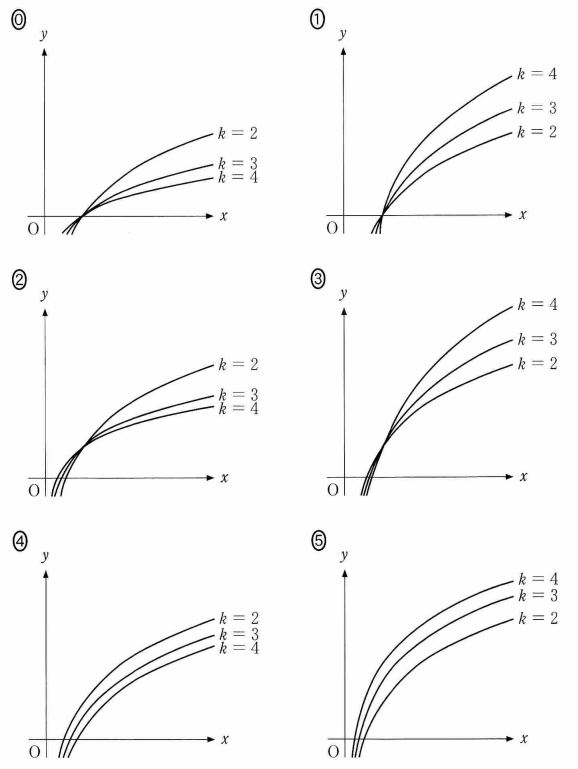
(iii) $k=2,3,4$ のとき

　$y=\log_k x$ のグラフの概形は $\dBox{カ}$
　$y=\log_2 kx$ のグラフの概形は $\dBox{キ}$

である。

　$\dbox{カ},\ \dbox{キ}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

(2) $x\gt 0,\ x\ne 1,\ y\gt 0$ とする。 $\log_x y$ について考えよう。

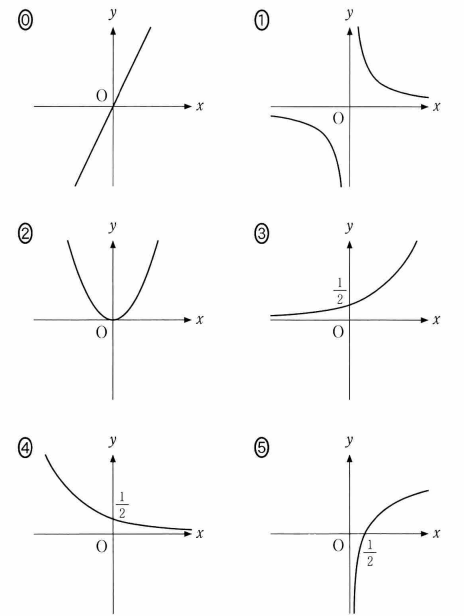
(i) 座標平面において、方程式 $\log_x y=2$ の表す図形を図示すると、 $\dBox{ク}$ の $x\gt 0,\ x\ne 1,\ y \gt 0$ の部分となる。

　$\dbox{ク}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つ選べ。

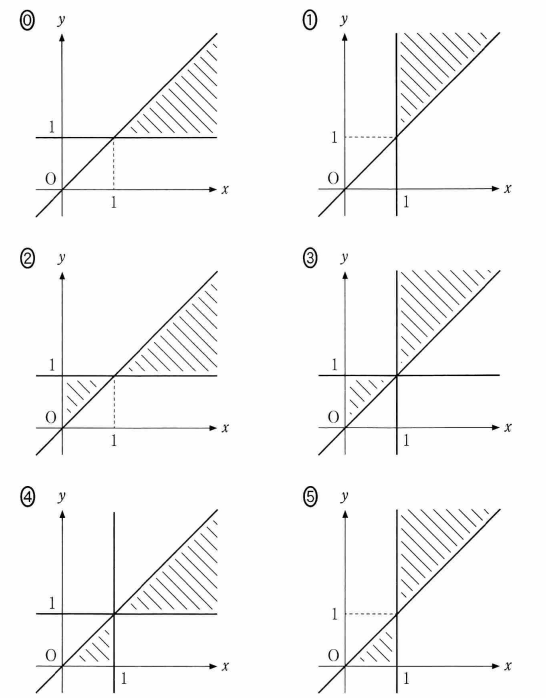
(ii) 座標平面において、不等式 $0\lt \log_x y\lt 1$ の表す領域を図示すると、 $\dBox{ケ}$ の斜線部分となる。ただし、境界（境界線）は含まない。

　$\dbox{ケ}$ については、最も適当なものとを次の 0 ～ 5 のうちから一つ選べ。

考え方

(1)の前半では、どういう点を通るかを考えますが、こうした情報を使って、グラフを選びましょう。対数のままで考えにくい場合は、変形してから考えましょう。

【必答問題】

解答編

問題

(1) $k\gt 0,\ k\ne 1$ とする。関数 $y=\log_k x$ と $y=\log_2 kx$ のグラフについて考えよう。

(i) $y=\log_3 x$ のグラフは点 $\left(27,\myBox{ア}\right)$ を通る。また、 $y=\log_2 \dfrac{x}{5}$ のグラフは点 $\left(\myBox{イウ},1\right)$ を通る。

解説

(1)
(i)
$\log_3 27=3$ なので、 $y=\log_3 x$ のグラフは、点 $(27,3)$ を通ります。

$1=\log_2\dfrac{x}{5}$ となるのは、 $\dfrac{x}{5}=2$ のときなので、 $x=10$ です。よって、 $y=\log_2\dfrac{x}{5}$ のグラフは、点 $(10,1)$ を通ります。

解答

ア：3 (1点)
イウ：10 (1点)

解答編　つづき

問題

(ii) $y=\log_k x$ のグラフは、 $k$ の値によらず定点 $\left(\myBox{エ},\ \myBox{オ}\right)$ を通る。

解説

(ii)
$y=\log_k x$ について、 $x=1$ のとき $y=0$ はどんな $k$ についても成り立つので、このグラフは、点 $(1,0)$ を通ります。

解答

エオ：10 (2点)

解答編　つづき

問題

(iii) $k=2,3,4$ のとき

　$y=\log_k x$ のグラフの概形は $\dBox{カ}$
　$y=\log_2 kx$ のグラフの概形は $\dBox{キ}$

である。

　$\dbox{カ},\ \dbox{キ}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。

解説

(iii)
$y=\log_k x$ のグラフは、まず $(1,0)$ を通るものを考えると、選択肢 0 と 1 だけが残ります。 $x=16$ とすると、 $k=2,4$ のときの値は、 $\log_2 16=4$ と $\log_4 16=2$ です。なので、 $x\gt 1$ の範囲で $k=2$ のグラフが上にあるものを選ぶと、整合的なものは選択肢 0 となります。

$y=\log_2 kx$ のグラフは、$x=1$ とすると、 $k=2,4$ のときの値は、 $\log_2 2=1$ と $\log_2 4=2$ です。 $k=4$ のときのほうが値が大きいことがわかります。

また、 $kx=1$ のときに $y=0$ となるので、 $k=2$ のときは $\left(\frac{1}{2},0\right)$ を通り、 $k=4$ のときは $\left(\frac{1}{4},0\right)$ を通ります。 $x$ 軸との交点は、 $k=2$ のグラフのほうが右にあります。整合的なものは選択肢 5 です。

解答

カ：0 (3点)
キ：5 (3点)

解答編　つづき

問題

(2) $x\gt 0,\ x\ne 1,\ y\gt 0$ とする。 $\log_x y$ について考えよう。

(i) 座標平面において、方程式 $\log_x y=2$ の表す図形を図示すると、 $\dBox{ク}$ の $x\gt 0,\ x\ne 1,\ y \gt 0$ の部分となる。

　$\dbox{ク}$ については、最も適当なものを、次の 0 ～ 5 のうちから一つ選べ。

解説

(2)
(i)
$\log_x y=2$ を変形すると $x^2=y$ なので、放物線 $y=x^2$ の一部となります。選択肢 2 です。

解答

ク：2 (2点)

解答編　つづき

問題

(ii) 座標平面において、不等式 $0\lt \log_x y\lt 1$ の表す領域を図示すると、 $\dBox{ケ}$ の斜線部分となる。ただし、境界（境界線）は含まない。

　$\dbox{ケ}$ については、最も適当なものとを次の 0 ～ 5 のうちから一つ選べ。

解説

(ii)
不等式 $0\lt \log_x y \lt 1$ の範囲を考えます。これを変形すると $\log_x 1 \lt \log_x y \lt \log_x x$ となります。

$x \gt 1$ のときは、この不等式は $1\lt y \lt x$ と同値です。なので、 $x\gt 1$ の範囲では、 $y=1$ より上で $y=x$ より下の部分が該当します。

$0 \lt x \lt 1$ のときは、この不等式は $1\gt y \gt x$ と同値です。なので、 $0\lt x\lt 1$ の範囲は、$y=x$ より上で $y=1$ より下の部分が該当します。

これらと整合的なものは、選択肢 2 です。

解答

ケ：2 (3点)