共通テスト数学I・数学A 2025年度第2問 [1] 解説

🕒 2025/01/19 🔄 2025/02/15

【必答問題】

問題編

問題

　花子さんと太郎さんは、公園にある二つの小さな噴水と一つの大きな噴水の高さについて話している。

あの中央の大きな噴水の高さは何メートルだろう。

実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。

じゃあ、放物線と仮定して、およその高さを考えてみよう。

　花子さんと太郎さんは、噴水の高さについて次のように考えることにした。

　噴水の水がえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1 のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1 の $\mathrm{P_1,P_2,P_3}$ は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。

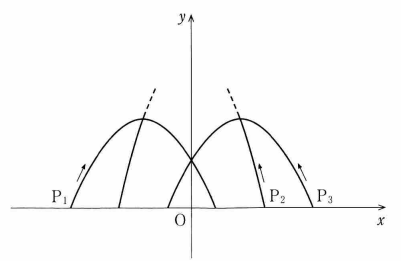
図1

仮定1

左側の小さな噴水の水がえがく放物線 $C_1$ は、$x$ 軸上の点 $\mathrm{P_1}\left(-\dfrac{5}{2},0\right)$ から出て点 $\left(\dfrac{1}{2},0\right)$ に至る。

右側の小さな噴水の水がえがく放物線 $C_3$ は、$x$ 軸上の点 $\mathrm{P_3}\left(\dfrac{5}{2},0\right)$ から出て点 $\left(-\dfrac{1}{2},0\right)$ に至る。

$C_1$ と $C_2$ はともに点 $(0,1)$ を通る。

仮定2
　中央の大きな噴水の水がえがく放物線 $C_1$ は、 $x$ 軸上の点 $\mathrm{P_2}\left(\dfrac{3}{2},0\right)$ から出て $C_3$ の頂点と $C_1$ の頂点を通る。

図1（再掲）

(1) 仮定1と仮定2のもとで考える。 $C_1$ をグラフにもつ2次関数を $y=ax^2+bx+c$ とする。このとき $c=\myBox{ア}$ であり、また\[ y=-\dfrac{\myBox{イ}}{\myBox{ウ}}x^2-\dfrac{\myBox{エ}}{\myBox{オ}}x+\mybox{ア} \]である。

　$C_1$ の頂点の $y$ 座標は $\dfrac{\myBox{カ}}{\myBox{キ}}$ である。このことを用いると、 $C_2$ の頂点の $y$ 座標は $\dfrac{\myBox{クケ}}{\myBox{コサ}}$ であることがわかる。

　したがって、大きな噴水の高さは、小さな噴水の高さの $\dBox{シ}$ である。

$\dbox{シ}$ については、最も適当なものを、次の 0 ～ 3 のうちから一つ選べ。

　0: およそ $2$ 倍
　1: およそ $3$ 倍
　2: およそ $4$ 倍
　3: およそ $5$ 倍

(2) 花子さんと太郎さんは、大きな噴水の高さについて話している。

正面から見たとき、大きな噴水が小さな噴水の頂点を通って見えるというデザインは変えずに、大きな噴水の高さを変えることはできるのかな。

左右の二つの小さな噴水は変えずに、大きな噴水の水が出る位置を変えてみたらどうかな。

大きな噴水の高さが $5$ メートルになるときの水が出る位置を考えてみよう。

　仮定2の代わりに次の仮定2'をおく。

仮定2'

中央の大きな噴水の水がえがく放物線 $C_2'$ は、$x$ 軸の正の部分の点 $\mathrm{P_2'}$ から出て $C_3$ の頂点と $C_1$ の頂点を通る。

$C_2'$ の頂点の $y$ 座標は $5$ である。

　仮定1と仮定2'のもとで考える。このとき、 $\mathrm{P_2}'$ は $\mathrm{P_2}$ より $\dfrac{\myBox{ス}}{\myBox{セ}}$ だけ $\dBox{ソ}$ の方にある。

$\dbox{ソ}$ の解答群

　0: $\mathrm{P_1}$
　1: $\mathrm{P_3}$

考え方

通る点から二次関数を特定するには、どの形が扱いやすいかを考えましょう。大きな噴水は $y$ 軸について対称であることもわかるので、このことも利用しましょう。

最後の問題では、高さを上げる・下げるには、噴水の水の出る位置をどちらに移動させるかを答えますが、方向だけなら日常生活から推測することもできるでしょう。

なお、実際に噴水を動かして確認できるツールを作ってみたので、使ってみてください。噴水デートアプリ 2025

【必答問題】

解答編

問題

　花子さんと太郎さんは、公園にある二つの小さな噴水と一つの大きな噴水の高さについて話している。

あの中央の大きな噴水の高さは何メートルだろう。

実際に高さを測定するのは難しそうだね。噴水の水がえがく曲線は、放物線になると聞いたことがあるよ。

じゃあ、放物線と仮定して、およその高さを考えてみよう。

　花子さんと太郎さんは、噴水の高さについて次のように考えることにした。

　噴水の水がえがく曲線は三つとも放物線とする。三つの噴水の水が出る位置は水平な地面にある。図1 のように座標軸が定められた平面上に、三つの噴水を正面から見た図をかく。左右の小さな噴水の水がえがく放物線については後の仮定1を、中央の大きな噴水の水がえがく放物線については後の仮定2を設定する。図1 の $\mathrm{P_1,P_2,P_3}$ は噴水の水が出る位置である。なお、長さの単位はメートルであるが、以下では省略する。

図1

仮定1

左側の小さな噴水の水がえがく放物線 $C_1$ は、$x$ 軸上の点 $\mathrm{P_1}\left(-\dfrac{5}{2},0\right)$ から出て点 $\left(\dfrac{1}{2},0\right)$ に至る。

右側の小さな噴水の水がえがく放物線 $C_3$ は、$x$ 軸上の点 $\mathrm{P_3}\left(\dfrac{5}{2},0\right)$ から出て点 $\left(-\dfrac{1}{2},0\right)$ に至る。

$C_1$ と $C_2$ はともに点 $(0,1)$ を通る。

仮定2
　中央の大きな噴水の水がえがく放物線 $C_1$ は、 $x$ 軸上の点 $\mathrm{P_2}\left(\dfrac{3}{2},0\right)$ から出て $C_3$ の頂点と $C_1$ の頂点を通る。

図1（再掲）

(1) 仮定1と仮定2のもとで考える。 $C_1$ をグラフにもつ2次関数を $y=ax^2+bx+c$ とする。このとき $c=\myBox{ア}$ であり、また\[ y=-\dfrac{\myBox{イ}}{\myBox{ウ}}x^2-\dfrac{\myBox{エ}}{\myBox{オ}}x+\mybox{ア} \]である。

解説

(1)

$C_1$ は $(0,1)$ を通るので、 $c=1$ です。

また、 $\left(-\frac{5}{2},0\right)$ と $\left(\frac{1}{2},0\right)$ を通ることから、 $C_1$ に対応する二次関数は
\begin{eqnarray} y &=& a\left(x+\frac{5}{2}\right)\left(x-\frac{1}{2}\right) \\[5pt] &=& a\left(x^2+2x-\frac{5}{4}\right) \end{eqnarray}と書けます。定数項は $1$ なので、 \begin{eqnarray} -\frac{5}{4}a &=& 1 \\[5pt] a &=& -\frac{4}{5} \\[5pt] \end{eqnarray}となることから \begin{eqnarray} y &=& -\frac{4}{5}\left(x^2+2x-\frac{5}{4}\right) \\[5pt] &=& -\frac{4}{5}x^2-\frac{8}{5}x+1 \end{eqnarray}となります。

解答

ア：1
イウエオ：4585

解答編　つづき

問題

　$C_1$ の頂点の $y$ 座標は $\dfrac{\myBox{カ}}{\myBox{キ}}$ である。このことを用いると、 $C_2$ の頂点の $y$ 座標は $\dfrac{\myBox{クケ}}{\myBox{コサ}}$ であることがわかる。

　したがって、大きな噴水の高さは、小さな噴水の高さの $\dBox{シ}$ である。

$\dbox{シ}$ については、最も適当なものを、次の 0 ～ 3 のうちから一つ選べ。

　0: およそ $2$ 倍
　1: およそ $3$ 倍
　2: およそ $4$ 倍
　3: およそ $5$ 倍

解説

$C_1$ の式を変形すると
\begin{eqnarray} y &=& -\frac{4}{5}\left(x^2+2x-\frac{5}{4}\right) \\[5pt] &=& -\frac{4}{5}\left\{(x+1)^2-1-\frac{5}{4}\right\} \\[5pt] &=& -\frac{4}{5}\left\{(x+1)^2-\frac{9}{4}\right\} \\[5pt] &=& -\frac{4}{5}(x+1)^2+\frac{9}{5} \\[5pt] \end{eqnarray}だから、頂点は $\left(-1,\frac{9}{5}\right)$ です。なので、頂点の $y$ 座標は $\dfrac{9}{5}$ だとわかります。

仮定2より、 $C_2$ は $\left(\dfrac{3}{2},0\right)$ を通り、対称性から、 $\left(-\dfrac{3}{2},0\right)$ も通ることがわかるので、 $C_2$ に対応する二次関数は
\begin{eqnarray} y&=& a\left(x-\frac{3}{2}\right)\left(x+\frac{3}{2}\right) \\[5pt] &=& a\left(x^2-\frac{9}{4}\right) \\[5pt] \end{eqnarray}と表せます。これが $\left(-1,\frac{9}{5}\right)$ を通るので、 \begin{eqnarray} \frac{9}{5} &=& a\left(1-\frac{9}{4}\right) \\[5pt] \frac{9}{5} &=& -\frac{5}{4}a \\[5pt] a &=& -\frac{36}{25} \\[5pt] \end{eqnarray}と求められるから、 $C_2$ に対応する二次関数は \begin{eqnarray} y &=& -\frac{36}{25}\left(x^2-\frac{9}{4}\right) \\[5pt] &=& -\frac{36}{25}x^2+\frac{81}{25} \\[5pt] \end{eqnarray}となります。

頂点の $y$ 座標は $\dfrac{81}{25}$ です。

頂点を比較すると、大きな噴水の高さを小さな噴水の高さで割って
\begin{eqnarray} \frac{81}{25} \div \frac{9}{5}=\frac{9}{5}=1.8 \end{eqnarray}なので、選択肢の中では「およそ2倍」が一番近いです。

解答

カキ：95
クケコサ：8125
シ：0

解答編　つづき

問題

(2) 花子さんと太郎さんは、大きな噴水の高さについて話している。

正面から見たとき、大きな噴水が小さな噴水の頂点を通って見えるというデザインは変えずに、大きな噴水の高さを変えることはできるのかな。

左右の二つの小さな噴水は変えずに、大きな噴水の水が出る位置を変えてみたらどうかな。

大きな噴水の高さが $5$ メートルになるときの水が出る位置を考えてみよう。

　仮定2の代わりに次の仮定2'をおく。

仮定2'

中央の大きな噴水の水がえがく放物線 $C_2'$ は、$x$ 軸の正の部分の点 $\mathrm{P_2'}$ から出て $C_3$ の頂点と $C_1$ の頂点を通る。

$C_2'$ の頂点の $y$ 座標は $5$ である。

　仮定1と仮定2'のもとで考える。このとき、 $\mathrm{P_2}'$ は $\mathrm{P_2}$ より $\dfrac{\myBox{ス}}{\myBox{セ}}$ だけ $\dBox{ソ}$ の方にある。

$\dbox{ソ}$ の解答群

　0: $\mathrm{P_1}$
　1: $\mathrm{P_3}$

解説

(2)

対称性より、 $C_2'$ に対応する二次関数は\[ y=ax^2+c \]と書けます。頂点の $y$ 座標を $5$ にすることから、 $c=5$ となります。

また、 $C_1$ の頂点 $\left(-1,\frac{9}{5}\right)$ を通るので
\begin{eqnarray} \frac{9}{5} &=& a\cdot(-1)^2+5 \\[5pt] a &=& -\frac{16}{5} \\[5pt] \end{eqnarray}となります。よって \begin{eqnarray} y &=& -\frac{16}{5}x^2+5 \\[5pt] &=& -\frac{16}{5}\left(x^2+\frac{25}{16}\right) \\[5pt] &=& -\frac{16}{5}\left(x+\frac{5}{4}\right)\left(x-\frac{5}{4}\right) \\[5pt] \end{eqnarray}が $C_2'$ に対応する二次関数です。

$\mathrm{P_2}$ の $x$ 座標は $\dfrac{3}{2}$ で、 $\mathrm{P_2'}$ の $x$ 座標は $\dfrac{5}{4}$ なので、 $\dfrac{5}{4}\lt\dfrac{3}{2}$ と\[ \dfrac{3}{2}-\dfrac{5}{4}=\dfrac{1}{4} \]だから、 $\mathrm{P_2'}$ は $\mathrm{P_2}$ より $\dfrac{1}{4}$ だけ $\mathrm{P_1}$ の方にあることがわかります。

なお、実際に噴水を動かして確認できるツールを作ってみたので、使ってみてください。噴水デートアプリ 2025