共通テスト 数学I・数学A 2017年度プレテスト 第4問 解説

2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【選択問題】(第3問～第5問から2問選択)

問題編

問題

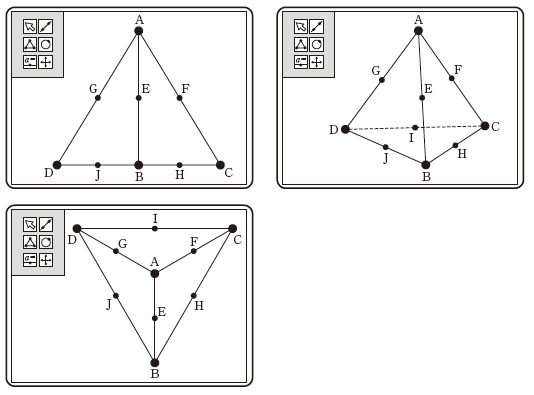
　花子さんと太郎さんは、正四面体ABCD の各辺の中点を次の図のようにE, F, G, H, I, J としたときに成り立つ性質について、コンピュータソフトを使いながら、下のように話している。二人の会話を読んで、下の問いに答えよ。

• 四角形FHJG は平行四辺形に見えるけれど、正方形ではないかな。
• 4辺の長さが等しいことは、簡単に証明できそうだよ。

(1) 太郎さんは四角形FHJG の4辺の長さが等しいことを、次のように証明した。

【太郎さんの証明】
　$\myBox{ア}$ により、四角形FHJG の各辺の長さはいずれも正四面体ABCD の１辺の長さの $\myBox{イ}$ 倍であるから、 ４辺の長さが等しくなる。

(i) $\myBox{ア}$ に当てはまる最も適当なものを、次の 0～4 のうちから一つ選べ。

　0: 中線定理
　1: 方べきの定理
　2: 三平方の定理
　3: 中点連結定理
　4: 円周角の定理

(ii) $\myBox{イ}$ に当てはまるものを、次の 0～4 のうちから一つ選べ。

　0: $2$

　1: $\dfrac{3}{4}$

　2: $\dfrac{2}{3}$

　3: $\dfrac{1}{2}$

　4: $\dfrac{1}{3}$

(2) 花子さんは、太郎さんの考えをもとに、正四面体をいろいろな方向から見て、四角形FHJG が正方形であることの証明について、下のような構想をもとに、実際に証明した。

【花子さんの構想】
　四角形において、４辺の長さが等しいことは正方形であるための $\myBox{ウ}$ 。さらに、対角線FJ とGH の長さが等しいことがいえれば、四角形FHJG が正方形であることの証明となるので、 $\triangle$ FJC と $\triangle$ GHD が合同であることを示したい。
　しかし、この二つの三角形が合同であることの証明は難しいので、別の三角形の組に着目する。

【花子さんの証明】
　点F、点G はそれぞれAC、AD の中点なので、二つの三角形 $\myBox{エ}$ と $\myBox{オ}$ に着目する。 $\mybox{エ}$ と $\mybox{オ}$ は３辺の長さがそれぞれ等しいので合同である。このとき、 $\mybox{エ}$ と $\mybox{オ}$ は $\myBox{カ}$ で、FとG はそれぞれAC、AD の中点なので、FJ = GH である。
　よって、四角形FHJG は、４辺の長さが等しく対角線の長さが等しいので正方形である。

(i) $\myBox{ウ}$ に当てはまるものを、次の 0～3 のうちから一つ選べ。

　0: 必要条件であるが十分条件でない
　1: 十分条件であるが必要条件でない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

(ii) $\myBox{エ}$, $\myBox{オ}$ に当てはまるものが、次の 0～5 の中にある。当てはまるものを一つずつ選べ。ただし、 $\mybox{エ}$ と $\mybox{オ}$ の解答の順序は問わない。

　0: $\triangle$ AGH
　1: $\triangle$ AIB
　2: $\triangle$ AJC
　3: $\triangle$ AHD
　4: $\triangle$ AHC
　5: $\triangle$ AJD

(iii) $\mybox{カ}$ に当てはまるものを、次の 0～3 のうちから一つ選べ。

　0: 正三角形
　1: 二等辺三角形
　2: 直角三角形
　3: 直角二等辺三角形

　四角形FHJG が正方形であることを証明した太郎さんと花子さんは、さらに、正四面体ABCD において成り立つ他の性質を見いだし、下のように話している。

• 線分EI と辺CD は垂直に交わるね。
• そう見えるだけかもしれないよ。証明できる？
• $_{(\mathrm{ a })}$ 辺CD は線分AI ともBI とも垂直だから、 $_{(\mathrm{ b })}$ 線分EI と辺CD は垂直といえるよ。
• そうか……。ということは、$_{(\mathrm{ c })}$ この性質は、四面体ABCD が正四面体でなくても成り立つ場合がありそうだね。

(3)　下線部(a) から下線部(b) を導く過程で用いる性質として正しいものを、次の 0～4 のうちからすべて選べ。 $\myBox{キ}$

　0: 平面$\alpha$ 上にある直線l と平面$\alpha$ 上にない直線m が平行ならば、 $\alpha /\!/ m$ である。

　1: 平面$\alpha$ 上にある直線l, m が点P で交わっているとき、点P を通り平面$\alpha$ 上にない直線n が直線l, m に垂直ならば、 $\alpha\perp n$ である。

　2: 平面$\alpha$ と直線l が点P で交わっているとき、 $\alpha\perp l$ ならば、平面 $\alpha$ 上の点P を通るすべての直線m に対して、 $l\perp m$ である。

　3: 平面$\alpha$ 上にある直線l, m がともに平面$\alpha$ 上にない直線n に垂直ならば、 $\alpha\perp n$ である。

　4: 平面 $\alpha$ 上に直線l、平面$\beta$ 上に直線m があるとき、 $\alpha\perp \beta$ ならば、 $l\perp m$ である。

(4) 下線部(c) について、太郎さんと花子さんは正四面体でない場合についても考えてみることにした。

　四面体ABCD において、AB、CD の中点をそれぞれE、I とするとき、下線部(b) が常に成り立つ条件について、次のように考えた。

　太郎さんが考えた条件：　AC = AD、BC = BD
　花子さんが考えた条件：　BC = AD、AC = BD

　四面体ABCD において、下線部(b) が成り立つ条件について正しく述べているものを、次の 0～3 のうちから一つ選べ。 $\myBox{ク}$

　0: 太郎さんが考えた条件、花子さんが考えた条件のどちらにおいても常に成り立つ。

　1: 太郎さんが考えた条件では常に成り立つが、花子さんが考えた条件では必ずしも成り立つとは限らない。

　2: 太郎さんが考えた条件では必ずしも成り立つとは限らないが、花子さんが考えた条件では常に成り立つ。

　3: 太郎さんが考えた条件、花子さんが考えた条件のどちらにおいても必ずしも成り立つとは限らない。

考え方

序盤の雰囲気から見ると簡単そうに感じますが、後半はかなりヘビーです。特に(3)(4)の難易度は高いです。

(3)は、今示そうとしていることが、一般的な言葉でどう表現されるかを考えないといけません。下線部(a)は3つの直線に関することなので、少なくとも3つの直線が出てくるものが関係しているだろう、などと推測してうまくつながるように試行錯誤しましょう。似たような選択肢ばかりで、混乱してきそうです。

(4)は、花子さんの条件をどう考えるかが重要です。下線部(a)は成り立ちませんが、だからといって下線部(b)が成り立たないとはいえません。本当に成り立たないかは、きちんと考える必要があります。

2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。

【選択問題】(第3問～第5問から2問選択)

解答編

問題

　花子さんと太郎さんは、正四面体ABCD の各辺の中点を次の図のようにE, F, G, H, I, J としたときに成り立つ性質について、コンピュータソフトを使いながら、下のように話している。二人の会話を読んで、下の問いに答えよ。

• 四角形FHJG は平行四辺形に見えるけれど、正方形ではないかな。
• 4辺の長さが等しいことは、簡単に証明できそうだよ。

(1) 太郎さんは四角形FHJG の4辺の長さが等しいことを、次のように証明した。

【太郎さんの証明】
　$\myBox{ア}$ により、四角形FHJG の各辺の長さはいずれも正四面体ABCD の１辺の長さの $\myBox{イ}$ 倍であるから、 ４辺の長さが等しくなる。

(i) $\myBox{ア}$ に当てはまる最も適当なものを、次の 0～4 のうちから一つ選べ。

　0: 中線定理
　1: 方べきの定理
　2: 三平方の定理
　3: 中点連結定理
　4: 円周角の定理

(ii) $\myBox{イ}$ に当てはまるものを、次の 0～4 のうちから一つ選べ。

　0: $2$

　1: $\dfrac{3}{4}$

　2: $\dfrac{2}{3}$

　3: $\dfrac{1}{2}$

　4: $\dfrac{1}{3}$

解説

例えば、三角形ABCと線分FHで考えてみましょう。

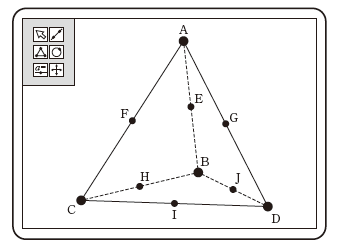
F, H は、それぞれ、辺 AC, BC の中点なので、使うのは中点連結定理ですね。これより、\[ \mathrm{ FH }=\frac{1}{2}\mathrm{ AB } \]となります。

他の面についても同様で、四角形FHJGの各辺の長さは、正四面体ABCDの1辺の長さの $\dfrac{1}{2}$ 倍になることがわかります。

解答

ア：3
イ：3

解答編 つづき

問題

(2) 花子さんは、太郎さんの考えをもとに、正四面体をいろいろな方向から見て、四角形FHJG が正方形であることの証明について、下のような構想をもとに、実際に証明した。

【花子さんの構想】
　四角形において、４辺の長さが等しいことは正方形であるための $\myBox{ウ}$ 。さらに、対角線FJ とGH の長さが等しいことがいえれば、四角形FHJG が正方形であることの証明となるので、 $\triangle$ FJC と $\triangle$ GHD が合同であることを示したい。
　しかし、この二つの三角形が合同であることの証明は難しいので、別の三角形の組に着目する。

【花子さんの証明】
　点F、点G はそれぞれAC、AD の中点なので、二つの三角形 $\myBox{エ}$ と $\myBox{オ}$ に着目する。 $\mybox{エ}$ と $\mybox{オ}$ は３辺の長さがそれぞれ等しいので合同である。このとき、 $\mybox{エ}$ と $\mybox{オ}$ は $\myBox{カ}$ で、FとG はそれぞれAC、AD の中点なので、FJ = GH である。
　よって、四角形FHJG は、４辺の長さが等しく対角線の長さが等しいので正方形である。

(i) $\myBox{ウ}$ に当てはまるものを、次の 0～3 のうちから一つ選べ。

　0: 必要条件であるが十分条件でない
　1: 十分条件であるが必要条件でない
　2: 必要十分条件である
　3: 必要条件でも十分条件でもない

(ii) $\myBox{エ}$, $\myBox{オ}$ に当てはまるものが、次の 0～5 の中にある。当てはまるものを一つずつ選べ。ただし、 $\mybox{エ}$ と $\mybox{オ}$ の解答の順序は問わない。

　0: $\triangle$ AGH
　1: $\triangle$ AIB
　2: $\triangle$ AJC
　3: $\triangle$ AHD
　4: $\triangle$ AHC
　5: $\triangle$ AJD

(iii) $\mybox{カ}$ に当てはまるものを、次の 0～3 のうちから一つ選べ。

　0: 正三角形
　1: 二等辺三角形
　2: 直角三角形
　3: 直角二等辺三角形

解説

まず、「４辺の長さが等しいことは正方形であるための何か？」ですね。「正方形なら4辺の長さが等しい」は正しいですが、逆は正しくありません。ひし形のときがありますからね。よって、「必要条件だが十分条件ではない」ことがわかります。

次に、花子さんの証明について考えましょう。途中で FJ=GH を示しているので、これに関連する三角形を使うんだな、と考えられます。この2つの線分を含んでいる三角形は、三角形AGH があります。しかし、証明の後の部分で「3辺の長さがそれぞれ等しいので」とあります。そもそも FJ=GH を示したいのだから、「3辺の長さがそれぞれ等しい」が先に出てくるのはおかしいです。なので、選択肢0 は不適切です。

ということで、 FJ, GH を辺に持つ三角形はダメだということがわかります。他の選択肢から選ぶのですが、これらの線分と異なる平面上にある三角形の場合、証明の続きを埋めていくことは難しそうです。この視点で、選択肢を消していきましょう。

そう考えると、FJと同じ平面上にある選択肢は、三角形AJC だけであることがわかります。 GHの場合は、三角形AHD だけであることがわかります。この2つの三角形の辺の長さは、正四面体の一辺の長さを $a$ とすると、どちらの三角形も\[ a,\frac{\sqrt{3} }{2}a,\frac{\sqrt{3} }{2}a \]となることがわかります。よって、確かに、合同になります。

また、この2つの三角形は、二等辺三角形であることもわかります。三平方の定理は成り立たないので、直角三角形ではありません。

解答

ウ：0
エオ：2,3
カ：1

解答編 つづき

問題

　四角形FHJG が正方形であることを証明した太郎さんと花子さんは、さらに、正四面体ABCD において成り立つ他の性質を見いだし、下のように話している。

• 線分EI と辺CD は垂直に交わるね。
• そう見えるだけかもしれないよ。証明できる？
• $_{(\mathrm{ a })}$ 辺CD は線分AI ともBI とも垂直だから、 $_{(\mathrm{ b })}$ 線分EI と辺CD は垂直といえるよ。
• そうか……。ということは、$_{(\mathrm{ c })}$ この性質は、四面体ABCD が正四面体でなくても成り立つ場合がありそうだね。

(3)　下線部(a) から下線部(b) を導く過程で用いる性質として正しいものを、次の 0～4 のうちからすべて選べ。 $\myBox{キ}$

　0: 平面$\alpha$ 上にある直線l と平面$\alpha$ 上にない直線m が平行ならば、 $\alpha /\!/ m$ である。

　1: 平面$\alpha$ 上にある直線l, m が点P で交わっているとき、点P を通り平面$\alpha$ 上にない直線n が直線l, m に垂直ならば、 $\alpha\perp n$ である。

　2: 平面$\alpha$ と直線l が点P で交わっているとき、 $\alpha\perp l$ ならば、平面 $\alpha$ 上の点P を通るすべての直線m に対して、 $l\perp m$ である。

　3: 平面$\alpha$ 上にある直線l, m がともに平面$\alpha$ 上にない直線n に垂直ならば、 $\alpha\perp n$ である。

　4: 平面 $\alpha$ 上に直線l、平面$\beta$ 上に直線m があるとき、 $\alpha\perp \beta$ ならば、 $l\perp m$ である。

解説

「辺CD は線分AI ともBI とも垂直だから」を表しているのは、選択肢1の「平面$\alpha$ 上にある直線l, m が点P で交わっているとき、点P を通り平面$\alpha$ 上にない直線n が直線l, m に垂直ならば」です。平面 $\alpha$ が三角形ABI を含む平面、直線 l, m が線分AI, BI、直線 n が辺CDに対応しています。

選択肢1の結論「 $\alpha\perp n$ 」に対応するものは、「三角形ABI を含む平面と辺CDが垂直」ですね。選択肢1の内容自体成り立ちますし、今の場合に適用することもできます。

このことと、下線部(b)の「線分EI と辺CD は垂直」を合わせると、選択肢2が対応していることがわかります。平面 $\alpha$ が三角形ABI を含む平面、直線 l が辺CDに対応しています。

よって、1と2を選ぶのが正解です。

選択肢0は、平行を使うところがないので不適です。選択肢4は、辺CDを含む平面について使えるものがないので不適です。

選択肢3がややこしいですが、直線l と m が異なるとは書いていません。2つの直線が同じ場合には、そもそも「 $\alpha\perp n$ 」が成り立たないので不適です。なお、選択肢2は、「点P で交わっている」とあるので、「2直線が異なること」が含まれています。

解答

キ：1, 2

解答編 つづき

問題

(4) 下線部(c) について、太郎さんと花子さんは正四面体でない場合についても考えてみることにした。

　四面体ABCD において、AB、CD の中点をそれぞれE、I とするとき、下線部(b) が常に成り立つ条件について、次のように考えた。

　太郎さんが考えた条件：　AC = AD、BC = BD
　花子さんが考えた条件：　BC = AD、AC = BD

　四面体ABCD において、下線部(b) が成り立つ条件について正しく述べているものを、次の 0～3 のうちから一つ選べ。 $\myBox{ク}$

　0: 太郎さんが考えた条件、花子さんが考えた条件のどちらにおいても常に成り立つ。

　1: 太郎さんが考えた条件では常に成り立つが、花子さんが考えた条件では必ずしも成り立つとは限らない。

　2: 太郎さんが考えた条件では必ずしも成り立つとは限らないが、花子さんが考えた条件では常に成り立つ。

　3: 太郎さんが考えた条件、花子さんが考えた条件のどちらにおいても必ずしも成り立つとは限らない。

解説

EIとCDが垂直に交わるかどうかを考えましょう。

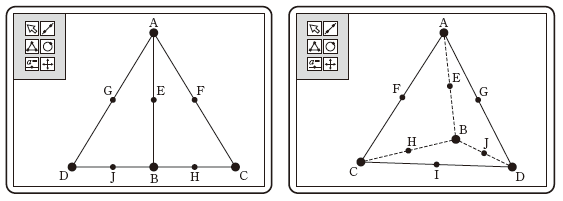
太郎さんの考えた条件のうち、 AC=AD から、AIとCDが垂直に交わることがわかります。三角形ACDが二等辺三角形で、Iが辺CDの中点だからです。また、 BC=BD から、 BIとCDが垂直に交わることも言えます。このことから、下線部(a)が成り立つことがわかるので、太郎さんの考えた条件では、下線部(b)が成り立つことがわかります。

花子さんの考えた条件、BC = AD、AC = BDを使うと、三角形ABCと三角形BADが合同であることがわかります。3組の辺がそれぞれ等しいからです。このことから、三角形ACEと三角形BDEも合同であることがわかります。2組の辺とその間の角がそれぞれ等しいからです。これより、三角形CDEは、CE=DEの二等辺三角形です。IはCDの中点だから、EIとCDが垂直に交わることがわかります。このときも下線部(b)が成り立ちます。

花子さんの条件でも成り立つことに気づくのは、難易度が高いです。

解答

ク：0