共通テスト 数学I・数学A 2017年度プレテスト 第3問 解説
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【選択問題】(第3問~第5問から2問選択)
問題編
問題
高速道路には、渋滞状況が表示されていることがある。目的地に行く経路が複数ある場合は、渋滞中を示す表示を見て経路を決める運転手も少なくない。太郎さんと花子さんは渋滞中の表示と車の流れについて、仮定をおいて考えてみることにした。
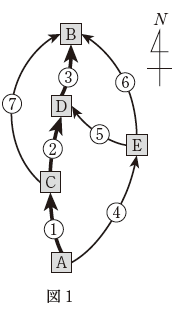
A 地点(入口)から B 地点(出口)に向かって北上する高速道路には、図1のように分岐点 A, C, E と合流点B, D がある。①, ②, ③は主要道路であり、④, ⑤, ⑥, ⑦ は迂回道路である。ただし、矢印は車の進行方向を表し、図1の経路以外に A 地点から B 地点に向かう経路はないとする。また、各分岐点 A, C, E には、それぞれ①と④, ②と⑦, ⑤と⑥の渋滞状況が表示される。
太郎さんと花子さんは、まず渋滞中の表示がないときに、A, C, E の各分岐点において運転手がどのような選択をしているか調査した。その結果が表1である。
表1 調査日 地点 台数 選択した道路 台数 5月10日 A 1183 ① 1092 ④ 91 5月11日 C 1008 ② 882 ⑦ 126 5月12日 E 496 ⑤ 248 ⑥ 248 これに対して太郎さんは、運転手の選択について、次のような仮定をおいて確率を使って考えることにした。
【太郎さんの仮定】
(i) 表1の選択の割合を確率とみなす。
(ii) 分岐点において、二つの道路のいずれにも渋滞中の表示がない場合、またはいずれにも渋滞中の表示がある場合、運転手が道路を選択する確率は(i)でみなした確率とする。
(iii) 分岐点において、片方の道路にのみ渋滞中の表示がある場合、運転手が渋滞中の表示のある道路を選択する確率は(i)でみなした確率の $\dfrac{2}{3}$ 倍とする。ここで、(i)の選択の割合を確率とみなすとは、例えば A 地点の分岐において④の道路を選択した割合 $\dfrac{91}{1183}=\dfrac{1}{13}$ を④の道路を選択する確率とみなすということである。
太郎さんの仮定のもとで、次の問いに答えよ。
(1) すべての道路に渋滞中の表示がない場合、A 地点の分岐において運転手が①の道路を選択する確率を求めよ。 $\dfrac{\myBox{アイ} }{\myBox{ウエ} }$
(2) すべての道路に渋滞中の表示がない場合、A 地点から B 地点に向かう車が D 地点を通過する確率を求めよ。 $\dfrac{\myBox{オカ} }{\myBox{キク} }$
(3) すべての道路に渋滞中の表示がない場合、A 地点から B 地点に向かう車で D 地点を通過した車が、E 地点を通過していた確率を求めよ。 $\dfrac{\myBox{ケ} }{\myBox{コサ} }$
(4) ①の道路にのみ渋滞中の表示がある場合、A 地点から B 地点に向かう車が D 地点を通過する確率を求めよ。 $\dfrac{\myBox{シス} }{\myBox{セソ} }$
各道路を通過する車の台数が1000台を超えると車の流れが急激に悪くなる。一方で各道路の通過台数が1000台を超えない限り、主要道路である①, ②, ③をより多くの車が通過することが社会の効率化に繋がる。したがって、各道路の通過台数が1000台を超えない範囲で、①, ②, ③をそれぞれ通過する台数の合計が最大になるようにしたい。
このことを踏まえて、花子さんは、太郎さんの仮定を参考にしながら、次のような仮定をおいて考えることにした。【花子さんの仮定】
(i) 分岐点において、二つの道路のいずれにも渋滞中の表示がない場合、またはいずれにも渋滞中の表示がある場合、それぞれの道路に進む車の割合は表1の割合とする。
(ii) 分岐点において、片方の道路にのみ渋滞中の表示がある場合、渋滞中の表示のある道路に進む車の台数の割合は表1の割合の $\dfrac{2}{3}$ 倍とする。過去のデータから5月13日に A 地点から B 地点に向かう車は1560台と想定している。そこで、花子さんの仮定のもとでこの台数を想定してシミュレーションを行った。このとき、次の問いに答えよ。
(5) すべての道路に渋滞中の表示がない場合、①を通過する台数は $\myBox{タチツテ}$ 台となる。よって、①の通過台数を1000台以下にするには、①に渋滞中の表示を出す必要がある。
①に渋滞中の表示を出した場合、①の通過台数は $\myBox{トナニ}$ 台となる。(6) 各道路の通過台数が1000台を超えない範囲で、①, ②, ③をそれぞれ通過する台数の合計を最大にするには、渋滞中の表示を $\myBox{ヌ}$ のようにすればよい。 $\myBox{ヌ}$ に当てはまるものを、次の 0~3 のうちから一つ選べ。
考え方
(1)(2)(4)は一般的な確率の問題で、和の法則・積の法則・余事象などを使って考えれば解くことができます。出題方法が変わっていますが、問題文の意味が読み取れれば、通常のセンター試験よりも計算の難易度は低めです。
(3)は条件付き確率ですが、これも標準的な内容です。
(5)(6)は、確率の問題というよりは、単なる割合の問題です。問題文にある条件が、どのような制約を表しているのか、正確に読み取る必要はありますが、計算自体は簡単です。
2017年11月に実施された、大学入試共通テスト導入に向けたプレテストの問題です。元の資料をできる限り再現していますが、一部でレイアウトが変わっています。画像は、大学入試センターのサイトから取得しています。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
高速道路には、渋滞状況が表示されていることがある。目的地に行く経路が複数ある場合は、渋滞中を示す表示を見て経路を決める運転手も少なくない。太郎さんと花子さんは渋滞中の表示と車の流れについて、仮定をおいて考えてみることにした。
A 地点(入口)から B 地点(出口)に向かって北上する高速道路には、図1のように分岐点 A, C, E と合流点B, D がある。①, ②, ③は主要道路であり、④, ⑤, ⑥, ⑦ は迂回道路である。ただし、矢印は車の進行方向を表し、図1の経路以外に A 地点から B 地点に向かう経路はないとする。また、各分岐点 A, C, E には、それぞれ①と④, ②と⑦, ⑤と⑥の渋滞状況が表示される。
太郎さんと花子さんは、まず渋滞中の表示がないときに、A, C, E の各分岐点において運転手がどのような選択をしているか調査した。その結果が表1である。
表1 調査日 地点 台数 選択した道路 台数 5月10日 A 1183 ① 1092 ④ 91 5月11日 C 1008 ② 882 ⑦ 126 5月12日 E 496 ⑤ 248 ⑥ 248 これに対して太郎さんは、運転手の選択について、次のような仮定をおいて確率を使って考えることにした。
【太郎さんの仮定】
(i) 表1の選択の割合を確率とみなす。
(ii) 分岐点において、二つの道路のいずれにも渋滞中の表示がない場合、またはいずれにも渋滞中の表示がある場合、運転手が道路を選択する確率は(i)でみなした確率とする。
(iii) 分岐点において、片方の道路にのみ渋滞中の表示がある場合、運転手が渋滞中の表示のある道路を選択する確率は(i)でみなした確率の $\dfrac{2}{3}$ 倍とする。ここで、(i)の選択の割合を確率とみなすとは、例えば A 地点の分岐において④の道路を選択した割合 $\dfrac{91}{1183}=\dfrac{1}{13}$ を④の道路を選択する確率とみなすということである。
太郎さんの仮定のもとで、次の問いに答えよ。
(1) すべての道路に渋滞中の表示がない場合、A 地点の分岐において運転手が①の道路を選択する確率を求めよ。 $\dfrac{\myBox{アイ} }{\myBox{ウエ} }$
解説
太郎さんの仮定(i)(ii)を用いて考えると、すべての道路に渋滞中の表示がない場合は、表1の選択の割合を確率とみなすことになります。
A 地点の分岐では、①か④を選ぶことになり、①を選ぶ割合は、表1の5月10日の部分を見ると\[ \frac{1092}{1183}=\frac{12}{13} \]となるので、これが求める確率となります。
解答
アイウエ:1213
解答編 つづき
問題
(2) すべての道路に渋滞中の表示がない場合、A 地点から B 地点に向かう車が D 地点を通過する確率を求めよ。 $\dfrac{\myBox{オカ} }{\myBox{キク} }$
解説
渋滞中の表示がない場合なので、選択の割合をそのまま確率とみなすのでしたね。
D を通過するのは、「A→C→D」と行く場合と「A→E→D」と行く場合の2通りあります。これらは別々のルートなので、それぞれの確率を足せば、D を通過する確率となります。
「A→C→D」と行くのは、A で①を選択し、 C で②を選択したときだけです。この選択をする確率は\[ \frac{1092}{1183} \times \frac{882}{1008}=\frac{12}{13} \times \frac{7}{8} =\frac{21}{26} \]となります。
「A→E→D」と行くのは、A で④を選択し、 E で⑤を選択したときだけです。この選択をする確率は\[ \frac{91}{1183} \times \frac{248}{496}=\frac{1}{13} \times \frac{1}{2} =\frac{1}{26} \]となります。
よって、求める確率は、この2つを足して\[ \frac{21}{26}+\frac{1}{26}=\frac{11}{13} \]となります。
解答
オカキク:1113
解答編 つづき
問題
(3) すべての道路に渋滞中の表示がない場合、A 地点から B 地点に向かう車で D 地点を通過した車が、E 地点を通過していた確率を求めよ。 $\dfrac{\myBox{ケ} }{\myBox{コサ} }$
解説
条件付き確率の問題です。
D を通過する確率は、(2)で求めた通り、 $\dfrac{11}{13}$ でした。また、「A→E→D→B」と通過する確率は、(2)を求める途中で得られた通り、 $\dfrac{1}{26}$ でした。よって、求める確率は\[ \frac{1}{26} \div \frac{11}{13} = \frac{1}{22} \]となります。
解答
ケコサ:122
参考
解答編 つづき
問題
(4) ①の道路にのみ渋滞中の表示がある場合、A 地点から B 地点に向かう車が D 地点を通過する確率を求めよ。 $\dfrac{\myBox{シス} }{\myBox{セソ} }$
解説
(2)で求めた確率を修正して考えればいいですね。
「A→C→D」と行くのは、A で①を選択し、 C で②を選択したときだけです。①を選ぶ確率が $\dfrac{2}{3}$ 倍になるので、この経路を選択する確率は\[ \frac{1092}{1183}\times \frac{2}{3} \times \frac{882}{1008}=\frac{21}{26} \times \frac{2}{3} =\frac{7}{13} \]となります。
A で④を選択する確率は、\[ 1-\frac{1092}{1183}\times \frac{2}{3}=1-\frac{8}{13}=\frac{5}{13} \]なので、「A→E→D」と行く確率は\[ \frac{5}{13}\times\frac{248}{496}=\frac{5}{26} \]となります。
よって、Dを通過する確率は\[ \frac{7}{13}+\frac{5}{26}=\frac{19}{26} \]となります。
解答
シスセソ:1926
解答編 つづき
問題
各道路を通過する車の台数が1000台を超えると車の流れが急激に悪くなる。一方で各道路の通過台数が1000台を超えない限り、主要道路である①, ②, ③をより多くの車が通過することが社会の効率化に繋がる。したがって、各道路の通過台数が1000台を超えない範囲で、①, ②, ③をそれぞれ通過する台数の合計が最大になるようにしたい。
このことを踏まえて、花子さんは、太郎さんの仮定を参考にしながら、次のような仮定をおいて考えることにした。【花子さんの仮定】
(i) 分岐点において、二つの道路のいずれにも渋滞中の表示がない場合、またはいずれにも渋滞中の表示がある場合、それぞれの道路に進む車の割合は表1の割合とする。
(ii) 分岐点において、片方の道路にのみ渋滞中の表示がある場合、渋滞中の表示のある道路に進む車の台数の割合は表1の割合の $\dfrac{2}{3}$ 倍とする。過去のデータから5月13日に A 地点から B 地点に向かう車は1560台と想定している。そこで、花子さんの仮定のもとでこの台数を想定してシミュレーションを行った。このとき、次の問いに答えよ。
(5) すべての道路に渋滞中の表示がない場合、①を通過する台数は $\myBox{タチツテ}$ 台となる。よって、①の通過台数を1000台以下にするには、①に渋滞中の表示を出す必要がある。
①に渋滞中の表示を出した場合、①の通過台数は $\myBox{トナニ}$ 台となる。
解説
すべての道路に渋滞中の表示がない場合、1560台の車のうち、①を通過する割合は $\dfrac{12}{13}$ なので\[ 1560\times \frac{12}{13}=1440 \]台であることがわかります。
もし①に渋滞中の表示を出した場合は、割合は $\dfrac{2}{3}$ 倍になるので、\[ 1440\times \dfrac{2}{3}=960 \]台となります。
解答
タチツテ:1440
トナニ:960
解答編 つづき
問題
(6) 各道路の通過台数が1000台を超えない範囲で、①, ②, ③をそれぞれ通過する台数の合計を最大にするには、渋滞中の表示を $\myBox{ヌ}$ のようにすればよい。 $\myBox{ヌ}$ に当てはまるものを、次の 0~3 のうちから一つ選べ。
解説
選択肢を見ると、A→Cの道が渋滞となっている場合しかありません。1560台のうち、Cに行く台数は先ほど求めた通り、960台、Eに行く台数は残りの600台です。
他の選択肢は、「C→Bに渋滞表示を出すか、C→Dに渋滞表示を出すか」と「E→Dに渋滞表示を出すか、E→Bに渋滞表示を出すか」の違いがあります。それぞれの場合を考えてみましょう。
C→Bに渋滞表示を出した場合、「A→C→D→B」と行く台数は、
\begin{eqnarray}
& &
960 \times \left(1-\frac{1}{8}\times\frac{2}{3}\right) \\[5pt]
&=&
960 \times \frac{11}{12} \\[5pt]
&=&
880 \\[5pt]
\end{eqnarray}台となります。
C→Dに渋滞表示を出した場合、「A→C→D→B」と行く台数は、
\begin{eqnarray}
& &
960 \times \frac{7}{8}\times\frac{2}{3} \\[5pt]
&=&
560 \\[5pt]
\end{eqnarray}台となります。
また、E→Dに渋滞表示を出した場合、「A→E→D→B」と行く台数は、
\begin{eqnarray}
& &
600 \times \frac{1}{2}\times\frac{2}{3} \\[5pt]
&=&
200 \\[5pt]
\end{eqnarray}台となります。
E→Bに渋滞表示を出した場合、「A→E→D→B」と行く台数は、
\begin{eqnarray}
& &
600 \times \left(1-\frac{1}{2}\times\frac{2}{3}\right) \\[5pt]
&=&
600 \times \frac{2}{3} \\[5pt]
&=&
400 \\[5pt]
\end{eqnarray}台となります。
以上から、条件に合うものを考えましょう。「各道路の通過台数が1000台を超えない」という条件は、D→Bの部分だけを考えればいいです。というのも、A→CもA→Eも1000台以下なので、その先の道を通過する車の台数は、合流するところ以外は1000台より少なくなるからです。
D→Bの部分の通過台数が1000台を超えることがあるかどうかを考えましょう。C→Bに渋滞表示を出した場合、C→Dを880台が通過します。一方、E→Dを200台以上通過するので、この場合は1000台を超えてしまいます。
C→Dに渋滞表示を出した場合、C→Dを560台が通過しますが、E→Dを通過するのは400台以下なので、この場合は1000台を超えることはありません。
以上から、C→Dに渋滞表示を出した場合だけを考えればいいです。このとき、D→Bのルートを通過する台数が多いのは、E→Bに渋滞表示を出した場合です。このとき、A→Cを860台、C→Dを560台、D→Bを960台の車が通り、①, ②, ③をそれぞれ通過する台数の合計が最大となります。
これに対応する選択肢は、3です。
解答
ヌ:3