京都大学 理学部特色入試 2018年度 第3問 解説
(2017年11月に行われた特色入試の問題です。2018年に行われた特色入試の問題はこちら)
問題編
問題
n を自然数とする。投げたとき表裏の出る確率がそれぞれ $\dfrac{1}{2}$ ずつであるような硬貨を用意し、この硬貨を $2^n-1$ 回投げる。このとき、 $2^{n-1}\leqq k\leqq 2^n-1$ である自然数 k のうち少なくとも1つが次の条件(*) を満たす確率を $p_n$ とする。
(*) n 以下のすべての自然数 m について、 $\left[ \dfrac{k}{2^{n-m} } \right]$ 回目の硬貨投げの結果は表である。
ただし、実数 x に対して、 $[x]$ は x より大きくない最大の整数を表す。
例えば、 $p_1$ は硬貨を1回投げて表が出る確率を表すので、 $p_1=\dfrac{1}{2}$ である。 $p_2$ は、硬貨を3回投げて、「1回目と2回目がともに表」であるか「1回目と3回目がともに表」であるかの少なくとも一方が成り立つ確率を表すので、 $p_2=\dfrac{3}{8}$ である。
以下の設問に答えよ。(1) $p_{n+1}$ を $p_n$ を用いて表せ。
(2) $r_n=\dfrac{2}{p_n}-n$ とする。すべての n に対して $r_n\geqq 3$ が成り立つことを示せ。
(3) すべての n に対して\[ \frac{2}{n+3+\log n} \leqq p_n \leqq \frac{2}{n+3} \]が成り立つことを示せ。
考え方
説明を読むと、(*)の条件がめんどくさそうです。で、その後の例を読むと、そこまでめんどくさくないかな、という気がしてきます。しかし、 $n=3$ のときを考えると、やっぱりめんどくさいことがわかってしまいます。
$n=3$ のときというのは、「1・2・4が表」「1・2・5が表」「1・3・6が表」「1・3・7が表」のどれかが成り立つときです。場合の数を考えようとしても、重なりが多すぎてダメです。普通に数えるわけにはいきません。工夫が必要です。
(1)を見れば、 $n+1$ 番目と $n$ 番目に関係がある、ということがわかりますが、パッとはわかりづらいですね。 $n+1$ のときを、「 $n$ までの場合と $n+1$ 番目」と分けるのではなく、「 $1$ 番目とそれ以降」という分け方にしたほうが考えやすいでしょう。ただ、答えを出しても、 $n=1,2$ のときしか確かめられないため、結果に不安は残ります。
(2)は、(1)の結果を使って、数学的帰納法で示そうとするのが王道でしょう。 $n=k$ のときをどう使うかを考えれば、どういう式変形をすればいいかはひらめきやすいです。
(3)は、(2)を変形すると、すぐに右側の不等式があらわれることに気づきます。これは、つまり、左側の不等式も、 $p_n$ をそのまま使うのではなく、逆数にして使う、というヒントととらえるといいでしょう。
今年の問題の中では、一番難しいです。
解答編
問題
n を自然数とする。投げたとき表裏の出る確率がそれぞれ $\dfrac{1}{2}$ ずつであるような硬貨を用意し、この硬貨を $2^n-1$ 回投げる。このとき、 $2^{n-1}\leqq k\leqq 2^n-1$ である自然数 k のうち少なくとも1つが次の条件(*) を満たす確率を $p_n$ とする。
(*) n 以下のすべての自然数 m について、 $\left[ \dfrac{k}{2^{n-m} } \right]$ 回目の硬貨投げの結果は表である。
ただし、実数 x に対して、 $[x]$ は x より大きくない最大の整数を表す。
例えば、 $p_1$ は硬貨を1回投げて表が出る確率を表すので、 $p_1=\dfrac{1}{2}$ である。 $p_2$ は、硬貨を3回投げて、「1回目と2回目がともに表」であるか「1回目と3回目がともに表」であるかの少なくとも一方が成り立つ確率を表すので、 $p_2=\dfrac{3}{8}$ である。
以下の設問に答えよ。(1) $p_{n+1}$ を $p_n$ を用いて表せ。
解答
(1)
以下のようにして、数字を並べていく。まず、 $1$ をおき、その右上に $2$ を、右下に $3$ を置く。そして、 $1$ と右上、右下とをそれぞれ線で結ぶ。以降、各自然数 i に対し、右上に $2i$ を、右下に $2i+1$ を置き、線で結んでいき、以下の図のようにする。
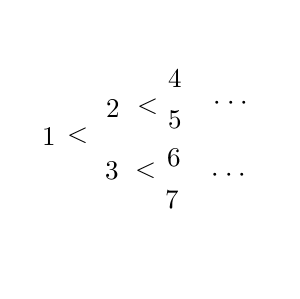
自然数 i を2進数表示したとき、一番右の数字に $0$ を追加したものが $2i$ で、 $1$ を追加したものが $2i+1$ であることから、左から n 列目には、上から順番に $2^{n-1}$ から $2^n-1$ の数字が1個ずつ並ぶことがわかる。また、 $\left[ \dfrac{k}{2^{n-m} } \right]$ は、 k を2進数表示したときの、右から $n-m$ 個の数字を取り除いたものになるため、上の並び方では、線をたどって $n-m$ 個左に移動した数字に対応する。
このことから、(*)の条件は、上の図で、「i 回目が表」となる数字 i だけを通って、左端から n 列目まで行ける道が存在することと同値である。
$p_{n+1}$ は、 $n+1$ 列目まで行ける確率である。これは、1回目が表であり、かつ、 $2$ か $3$ を通って $n+1$ 列目まで行ける確率と等しい。 $2$ の道の先にある数字は、2進数で表したときに上から2つ目の位の数字が $0$ である数である。この $0$ を取り除けば、 $1$ から $n$ 列目までの道と構造が同じであることがわかるため、 $2$ を通って $n+1$ 列目まで行ける確率は $p_n$ となる。同様に、 $3$ の道の先にある数字は、2進数で表したときに上から2つ目の位の数字が $1$ であり、これも同じ構造であることから、 $3$ を通って $n+1$ 列目まで行ける確率は $p_n$ となる。
また、「i 回目が表」となる数字だけを通って $1$ から $n+1$ 列目まで行ける道のうち、 $2$ を通る道も $3$ を通る道も存在する確率は、 $2$ の道の先と $3$ の道の先にある数字にダブりがないことから、 $p_n^2$ であることがわかる。
以上から
\begin{eqnarray}
p_{n+1}
&=&
\frac{1}{2} \times \left( p_n +p_n -p_n^2 \right) \\[5pt]
&=&
p_n-\frac{1}{2}p_n^2 \\[5pt]
\end{eqnarray}となることがわかる。
問題
(2) $r_n=\dfrac{2}{p_n}-n$ とする。すべての n に対して $r_n\geqq 3$ が成り立つことを示せ。
解答
(2)
(i) $n=1$ のとき
\begin{eqnarray}
r_1
&=&
\frac{2}{p_1}-1 \\[5pt]
&=&
4-1 \\[5pt]
&\geqq&
3 \\[5pt]
\end{eqnarray}となる。
(ii) $n=k$ のとき $r_k\geqq 3$ とすると、 $\dfrac{2}{p_k}\geqq k+3$ が成り立つので
\begin{eqnarray}
r_{k+1}
&=&
\frac{2}{p_{k+1} }-(k+1) \\[5pt]
&=&
\frac{2}{p_k-\frac{1}{2}p_k^2}-k-1 \\[5pt]
&=&
\frac{4}{p_k(2-p_k)}-k-1 \\[5pt]
&=&
\frac{2}{p_k}+\frac{2}{2-p_k}-k-1 \\[5pt]
&\geqq &
(k+3)-k-1+\frac{2}{2-p_k} \\[5pt]
&\geqq &
2+1+\frac{p_k}{2-p_k} \\[5pt]
&\geqq &
3 \\[5pt]
\end{eqnarray}なので、 $n=k+1$ のときも $r_{k+1}\geqq 3$ が成り立つ。
(i)(ii)から、すべての自然数 n に対して $r_n\geqq 3$ が成り立つ。
問題
(3) すべての n に対して\[ \frac{2}{n+3+\log n} \leqq p_n \leqq \frac{2}{n+3} \]が成り立つことを示せ。
解答
(3)
(2)より
\begin{eqnarray}
& &
\frac{2}{p_n}-n \geqq 3 \\[5pt]
&\iff&
\frac{1}{p_n} \geqq \frac{n+3}{2} \\[5pt]
&\iff&
p_n \leqq \frac{2}{n+3} \\[5pt]
\end{eqnarray}となるので、右側の不等号は成り立つ。
左側の不等式 $\frac{2}{n+3+\log n} \leqq p_n$ を示す。これは
\begin{eqnarray}
& &
\frac{2}{n+3+\log n} \leqq p_n \\[5pt]
&\iff&
n+3+\log n \geqq \frac{2}{p_n} \\[5pt]
\end{eqnarray}となるので、最後の不等式を数学的帰納法で示す。
(i) $n=1$ のとき、
\begin{eqnarray}
1+3+\log 1 - \frac{2}{p_1}=4-4=0
\end{eqnarray}より、成り立つ。
(ii) $n=k$ のとき、 $k+3+\log k \geqq \frac{2}{p_k}$ が成り立つとする。 $n=k+1$ のときは
\begin{eqnarray}
& &
(k+1)+3+\log (k+1) -\frac{2}{p_{k+1} } \\[5pt]
&=&
k+4+\log (k+1) -\frac{2}{p_k-\frac{1}{2}p_k^2} \\[5pt]
&=&
k+4+\log (k+1) -\frac{2}{p_k}-\frac{2}{2-p_k} \\[5pt]
\end{eqnarray}ここで、仮定より、
\begin{eqnarray}
& &
k+4+\log (k+1) -\frac{2}{p_k}-\frac{2}{2-p_k} \\[5pt]
&\geqq&
k+4+\log (k+1) -(k+3+\log k)-\frac{2}{2-p_k} \\[5pt]
&=&
1+\log (k+1) -\log k -1-\frac{p_k}{2-p_k} \\[5pt]
&=&
\log (k+1) -\log k-\frac{p_k}{2-p_k} \\[5pt]
\end{eqnarray}となる。ここで、
\begin{eqnarray}
\log (k+1) -\log k
&=&
\int_k^{k+1}\frac{1}{x}dx \\[5pt]
&\geqq &
\int_k^{k+1}\frac{1}{k+1}dx \\[5pt]
&\geqq &
\frac{1}{k+1} \\[5pt]
\end{eqnarray}であり、
\begin{eqnarray}
& &
p_n \leqq \frac{2}{n+3} \\[5pt]
&\iff&
\frac{2}{p_n} \geqq n+3 \\[5pt]
&\iff&
\frac{2}{p_n}-1 \geqq n+2 \\[5pt]
&\iff&
-\frac{1}{\frac{2}{p_n}-1} \geqq -\frac{1}{n+2} \\[5pt]
&\iff&
-\frac{p_n}{2-p_n} \geqq -\frac{1}{n+2} \\[5pt]
\end{eqnarray}が成り立つので、
\begin{eqnarray}
& &
\log (k+1) -\log k-\frac{p_k}{2-p_k} \\[5pt]
&\geqq &
\frac{1}{k+1}-\frac{1}{k+2} \\[5pt]
&\geqq &
0
\end{eqnarray}が成り立つ。よって、 $n=k+1$ のときも成り立つ。
(i)(ii)より、左側の不等式も成り立つことがわかる。
以上から、すべての自然数 n に対して\[ \frac{2}{n+3+\log n} \leqq p_n \leqq \frac{2}{n+3} \]が成り立つ。
(解答終)
解説
$n=3$ のときは、「1・2・4が表」「1・2・5が表」「1・3・6が表」「1・3・7が表」のどれかが成り立つときです。どの場合も「1が表」ですね。「1が表」という条件を付けると、あとは、「2・4が表」「2・5が表」「3・6が表」「3・7が表」の確率を計算できればいいですね。ここで、前半2つと後半2つにダブりがないこと、前半2つも後半2つも「1・2が表、または、1・3が表」という構造になっていることを利用して考えましょう。(1)の説明は、かなり書きにくいと思います。





