京都大学 理学部特色入試 2018年度 第1問 解説
(2017年11月に行われた特色入試の問題です。2018年に行われた特色入試の問題はこちら)
問題編
問題
凸五角形 $\mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n$ $(n=1,2,\cdots)$ が次の条件を満たしている。
$\mathrm{A}_{n+1}$ は辺 $\mathrm{C}_n\mathrm{D}_n$ の中点
$\mathrm{B}_{n+1}$ は辺 $\mathrm{D}_n\mathrm{E}_n$ の中点
$\mathrm{C}_{n+1}$ は辺 $\mathrm{E}_n\mathrm{A}_n$ の中点
$\mathrm{D}_{n+1}$ は辺 $\mathrm{A}_n\mathrm{B}_n$ の中点
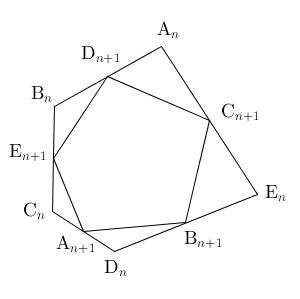
$\mathrm{E}_{n+1}$ は辺 $\mathrm{B}_n\mathrm{C}_n$ の中点下図は、五角形 $\mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n$ と五角形 $\mathrm{A}_{n+1}\mathrm{B}_{n+1}\mathrm{C}_{n+1}\mathrm{D}_{n+1}\mathrm{E}_{n+1}$ の位置関係を図示したものである。
以下の設問に答えよ。(1) 正の実数 $\alpha$ をうまく取ると、数列 $\left\{ \alpha^n \left| \overrightarrow{ \mathrm{A}_n\mathrm{B}_n } \right| \right\}$ が $0$ でない実数に収束するようにできることを示せ。
(2) 五角形 $\mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n$ の5本の辺の長さの和を $L_n$ 、5本の対角線の長さの和を $M_n$ とする。極限値 $\displaystyle \lim_{n\to \infty} \frac{M_n}{L_n}$ を求めよ。
ただし、五角形が凸であるとは、その内角がすべて $180^{\circ}$ 未満であることをいう。また、五角形の対角線とは、2頂点を結ぶ線分で辺でないもののことである。
考え方
とりあえず、正五角形について考えれば、答えの推測はできます。(2)の答えは、黄金比だろう、という予想はつきます。
ただ、一般の五角形で考えていくのは、なかなか難しいです。 $\mathrm{A}_{n+1}\mathrm{B}_{n+1}$ と $\mathrm{C}_n\mathrm{E}_n$ との関係はすぐにわかりますが、 $\mathrm{C}_n\mathrm{E}_n$ は少しいじりにくいですね。少し気づきにくいですが、 $\overrightarrow{ \mathrm{C}_n\mathrm{E}_n }$ に関する漸化式を作りましょう。
漸化式さえできれば、ベクトルの列の一般項を求めましょう。あまり出てこないですが、考え方としては数列と同じようにすればいいですね。一般項は、どこかで見たことがある形になります。一般項が分かれば、 $0$ でない値に収束するために、 $\alpha$ をいくらにすればいいかはすぐにわかります。収束値が $0$ でないことを確認しましょう。
(1)ができれば、(2)はそんなに難しくはありません。
解答編
問題
凸五角形 $\mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n$ $(n=1,2,\cdots)$ が次の条件を満たしている。
$\mathrm{A}_{n+1}$ は辺 $\mathrm{C}_n\mathrm{D}_n$ の中点
$\mathrm{B}_{n+1}$ は辺 $\mathrm{D}_n\mathrm{E}_n$ の中点
$\mathrm{C}_{n+1}$ は辺 $\mathrm{E}_n\mathrm{A}_n$ の中点
$\mathrm{D}_{n+1}$ は辺 $\mathrm{A}_n\mathrm{B}_n$ の中点
$\mathrm{E}_{n+1}$ は辺 $\mathrm{B}_n\mathrm{C}_n$ の中点下図は、五角形 $\mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n$ と五角形 $\mathrm{A}_{n+1}\mathrm{B}_{n+1}\mathrm{C}_{n+1}\mathrm{D}_{n+1}\mathrm{E}_{n+1}$ の位置関係を図示したものである。
以下の設問に答えよ。(1) 正の実数 $\alpha$ をうまく取ると、数列 $\left\{ \alpha^n \left| \overrightarrow{ \mathrm{A}_n\mathrm{B}_n } \right| \right\}$ が $0$ でない実数に収束するようにできることを示せ。
(2) 五角形 $\mathrm{A}_n\mathrm{B}_n\mathrm{C}_n\mathrm{D}_n\mathrm{E}_n$ の5本の辺の長さの和を $L_n$ 、5本の対角線の長さの和を $M_n$ とする。極限値 $\displaystyle \lim_{n\to \infty} \frac{M_n}{L_n}$ を求めよ。
ただし、五角形が凸であるとは、その内角がすべて $180^{\circ}$ 未満であることをいう。また、五角形の対角線とは、2頂点を結ぶ線分で辺でないもののことである。
解答
(1)
平面上に点 O をとり、O に関する位置ベクトルを考える。
条件から、任意の自然数 n に対して
\begin{eqnarray}
\overrightarrow{ \mathrm{A}_{n+1}\mathrm{B}_{n+1} }
&=&
\overrightarrow{ \mathrm{O}\mathrm{B}_{n+1} }-\overrightarrow{ \mathrm{O}\mathrm{A}_{n+1} } \\[5pt]
&=&
\frac{1}{2}\left( \overrightarrow{ \mathrm{O}\mathrm{D}_n }+\overrightarrow{ \mathrm{O}\mathrm{E}_n } \right)
-\frac{1}{2}\left( \overrightarrow{ \mathrm{O}\mathrm{C}_n }+\overrightarrow{ \mathrm{O}\mathrm{D}_n } \right)
\\[5pt]
&=&
\frac{1}{2}\overrightarrow{ \mathrm{C}_n\mathrm{E}_n } \\[5pt]
\end{eqnarray}が成り立つ。よって、任意の自然数 n に対して
\begin{eqnarray}
\overrightarrow{ \mathrm{C}_{n+2}\mathrm{E}_{n+2} }
&=&
\overrightarrow{ \mathrm{O}\mathrm{E}_{n+2} }-\overrightarrow{ \mathrm{O}\mathrm{C}_{n+2} } \\[5pt]
&=&
\frac{1}{2}\left( \overrightarrow{ \mathrm{O}\mathrm{B}_{n+1} }+\overrightarrow{ \mathrm{O}\mathrm{C}_{n+1} } \right)
-\frac{1}{2}\left( \overrightarrow{ \mathrm{O}\mathrm{E}_{n+1} }+\overrightarrow{ \mathrm{O}\mathrm{A}_{n+1} } \right) \\[5pt]
&=&
\frac{1}{2}\overrightarrow{ \mathrm{A}_{n+1}\mathrm{B}_{n+1} }
+\frac{1}{2}\overrightarrow{ \mathrm{E}_{n+1}\mathrm{C}_{n+1} } \\[5pt]
&=&
\frac{1}{4}\overrightarrow{ \mathrm{C}_n\mathrm{E}_n }
-\frac{1}{2}\overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} } \\[5pt]
\end{eqnarray}が成り立つ。
ここで、\[ x^2+\frac{1}{2}x-\frac{1}{4}=0 \]とすると、\[ x=\frac{-1\pm\sqrt{5} }{4} \]が得られる。この解を\[ p=\frac{-1-\sqrt{5} }{4},\ q=\frac{-1+\sqrt{5} }{4} \]とおくと、次の2つの式が、任意の自然数 n に対して成り立つ。
\begin{eqnarray}
\overrightarrow{ \mathrm{C}_{n+2}\mathrm{E}_{n+2} }
-p \overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} }
&=&
q ( \overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} }
-p \overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} } )
\\[5pt]
\overrightarrow{ \mathrm{C}_{n+2}\mathrm{E}_{n+2} }
-q \overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} }
&=&
p ( \overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} }
-q \overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} } ) \\[5pt]
\end{eqnarray}これより、
\begin{eqnarray}
\overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} }
-p \overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} }
&=&
q^{n-1} ( \overrightarrow{ \mathrm{C}_{2}\mathrm{E}_{2} }
-p \overrightarrow{ \mathrm{C}_{1}\mathrm{E}_{1} } )
\\[5pt]
\overrightarrow{ \mathrm{C}_{n+1}\mathrm{E}_{n+1} }
-q \overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} }
&=&
p^{n-1} ( \overrightarrow{ \mathrm{C}_{2}\mathrm{E}_{2} }
-q \overrightarrow{ \mathrm{C}_{1}\mathrm{E}_{1} } ) \\[5pt]
\end{eqnarray}が成り立つ。この式を辺々引けば、
\begin{eqnarray}
\overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} }
&=&
q^n \frac{ \overrightarrow{ \mathrm{C}_2\mathrm{E}_2 } -p\overrightarrow{ \mathrm{C}_1\mathrm{E}_1 } }{q(q-p)}
-p^n \frac{ \overrightarrow{ \mathrm{C}_2\mathrm{E}_2 } -q\overrightarrow{ \mathrm{C}_1\mathrm{E}_1 } }{p(q-p)}
\end{eqnarray}が得られる。
ここで、\[ \vec{v_1} = \frac{ \overrightarrow{ \mathrm{C}_2\mathrm{E}_2 } -p\overrightarrow{ \mathrm{C}_1\mathrm{E}_1 } }{q(q-p)}, \ \vec{v_2} = \frac{ \overrightarrow{ \mathrm{C}_2\mathrm{E}_2 } -q\overrightarrow{ \mathrm{C}_1\mathrm{E}_1 } }{p(q-p)} \]とすると、
\begin{eqnarray}
\Big| |q^n| |v_1| -|p^n| |v_2| \Big|
\leqq
|\overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} }|
\leqq
|q^n| |v_1| +|p^n| |v_2|
\end{eqnarray}が成り立つ。
もし、 $|v_2|=0$ だとすると、 $\overrightarrow{ \mathrm{C}_2\mathrm{E}_2 } =q\overrightarrow{ \mathrm{C}_1\mathrm{E}_1 }$ が成り立つ。また、 $\overrightarrow{ \mathrm{A}_2\mathrm{B}_2 } =\frac{1}{2}\overrightarrow{ \mathrm{C}_1\mathrm{E}_1 }$ も成り立つので、\[ \overrightarrow{ \mathrm{C}_2\mathrm{E}_2 } = 2q\overrightarrow{ \mathrm{A}_2\mathrm{B}_2 } \]が成り立つ。ここで、 $q=\dfrac{-1+\sqrt{5} }{4} \gt 0$ であることから、 $\overrightarrow{ \mathrm{A}_2\mathrm{B}_2 }$ と $\overrightarrow{ \mathrm{C}_2\mathrm{E}_2 }$ は、平行で向きが同じベクトルとなる。しかし、そうすると、五角形の辺である $\mathrm{A}_2\mathrm{E}_2$ と $\mathrm{B}_2\mathrm{C}_2$ が交わってしまう。そのため、\[ |v_2|\ne 0 \]となる。
また、
\begin{eqnarray}
\left| \frac{q}{p} \right|=\frac{\sqrt{5}-1}{\sqrt{5}+1} \lt 1
\end{eqnarray}であることにも注意すると、上の不等式とはさみうちの原理から
\begin{eqnarray}
\lim_{n\to \infty} \frac{1}{|p|^n}|\overrightarrow{ \mathrm{C}_{n}\mathrm{E}_{n} }|
&=&
|v_2| \ne 0
\end{eqnarray}となることがわかる。このことと、
\begin{eqnarray}
\overrightarrow{ \mathrm{A}_{n+1}\mathrm{B}_{n+1} }
&=&
\frac{1}{2}\overrightarrow{ \mathrm{C}_n\mathrm{E}_n } \\[5pt]
\end{eqnarray}より、 $\alpha$ を $\dfrac{1}{|p|}=\dfrac{4}{\sqrt{5}+1}=\sqrt{5}-1$ とすれば、数列 $\left\{ \alpha^n \left| \overrightarrow{ \mathrm{A}_n\mathrm{B}_n } \right| \right\}$ が $0$ でない実数に収束するようにできることがわかる。
(2)
(1) の p, q, $v_1$ $v_2$ について、
\begin{eqnarray}
\lim_{n\to\infty} \frac{\mathrm{C}_n\mathrm{E}_n}{\mathrm{A}_n\mathrm{B}_n}
&=&
\lim_{n\to\infty} \frac{\mathrm{C}_n\mathrm{E}_n}{\frac{1}{2}\mathrm{C}_{n-1}\mathrm{E}_{n-1} } \\[5pt]
&=&
\lim_{n\to\infty} 2\times \frac{\frac{1}{|p|^{n} }\mathrm{C}_n\mathrm{E}_n}{\frac{1}{|p|^{n} }\mathrm{C}_{n-1}\mathrm{E}_{n-1} } \\[5pt]
&=&
\lim_{n\to\infty} 2|p|\times \frac{\frac{1}{|p|^{n} }\mathrm{C}_n\mathrm{E}_n}{\frac{1}{|p|^{n-1} }\mathrm{C}_{n-1}\mathrm{E}_{n-1} } \\[5pt]
&=&
2|p|\times \frac{|v_2|}{|v_2|} \\[5pt]
&=&
\frac{1+\sqrt{5} }{2}
\end{eqnarray}となる。(1)と同様の議論により、他の辺・対角線についても同様に収束することがわかることから
\begin{eqnarray}
\lim_{n\to\infty} \frac{M_n}{L_n}
&=&
\lim_{n\to\infty} 2|p| \times \frac{\frac{1}{|p|^n}\times M_n}{\frac{1}{|p|^{n-1} }\times M_{n-1} } \\[5pt]
&=&
2|p| \\[5pt]
&=&
\frac{1+\sqrt{5} }{2}
\end{eqnarray}が得られる。
(解答終)
解説
(1)は、 $\overrightarrow{ \mathrm{C}_n\mathrm{E}_n }$ に関する漸化式を作る必要があります( $\overrightarrow{ \mathrm{A}_{n}\mathrm{B}_{n} }$ に関して作ってもいいです)。3項の漸化式が得られるので、これを一般的な形で解くと、 $p^n$ が出てきます。収束値が $0$ にならないことに言及して、 $\alpha$ を求めましょう。
(2)は、分母・分子を同じ文字で割って収束するため、収束する値もすぐに求められます。