京都大学 理学部特色入試 2018年度 第2問 解説
(2017年11月に行われた特色入試の問題です。2018年に行われた特色入試の問題はこちら)
問題編
問題
実数 a, b が $0\leqq a \lt 1$ および $0\leqq b\lt 1$ を満たしている。このとき、次の条件 (C) を満たす2つの整数 m, n が存在することを示せ。
(C) xy 平面において、点 $(m+a,n+b)$ を中心とする半径 $\dfrac{1}{100}$ の円の内部が、 $y=x^2$ のグラフと共有点を持つ。
考え方
「円と共有点を持つ」となっていますが、この条件はもっと緩くできます。結局、 $(\sqrt{n+b},n+b)$ との距離を考えればよく、うまく $m,n$ を選べば、 $m+a$ と $\sqrt{n+b}$ との差が $\dfrac{1}{100}$ 未満になることを示す、と考えたほうが取り組みやすいでしょう。
解答編
問題
実数 a, b が $0\leqq a \lt 1$ および $0\leqq b\lt 1$ を満たしている。このとき、次の条件 (C) を満たす2つの整数 m, n が存在することを示せ。
(C) xy 平面において、点 $(m+a,n+b)$ を中心とする半径 $\dfrac{1}{100}$ の円の内部が、 $y=x^2$ のグラフと共有点を持つ。
解答
$m=50$ とする。
$m$ と $m+1$ の間を $\sqrt{m^2+j}$ $(j=1,2,\cdots, 2m)$ で区切る。
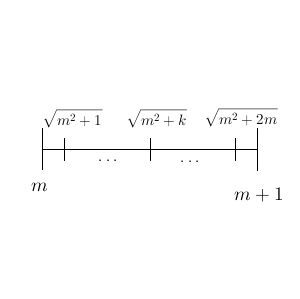
このとき、この各区間(左端を含み、右端を含まない)のどこか1つに、 $m+a$ が含まれる。つまり、 a に対して、次を満たす整数 k $(0\leqq k \leqq 2m)$ がただ1つ存在する。\[ \sqrt{m^2+k} \leqq m+a \lt \sqrt{m^2+k+1} \]
また、 $n=m^2+k$ とすると、\[ m^2+k \leqq n+b \lt m^2+k+1 \]が成り立つ。
今、 $y=x^2$ 上の点 $(\sqrt{n+b},n+b)$ と点 $(m+a,n+b)$ との距離を考えると
\begin{eqnarray}
& &
|\sqrt{n+b}-(m+a)| \\[5pt]
&\lt&
\sqrt{m^2+k+1}-\sqrt{m^2+k} \\[5pt]
&=&
\frac{1}{\sqrt{m^2+k+1}+\sqrt{m^2+k} } \\[5pt]
&\lt&
\frac{1}{\sqrt{m^2}+\sqrt{m^2} } \\[5pt]
&=&
\frac{1}{2m} \\[5pt]
&=&
\frac{1}{100} \\[5pt]
\end{eqnarray}となる。
よって、上のように $m,n$ を選べば、 $y=x^2$ 上の点 $(\sqrt{n+b},n+b)$ と点 $(m+a,n+b)$ との距離を $\dfrac{1}{100}$ 未満にできるので、(C)を満たす $m,n$ が存在することがわかる。
(解答終)





