センター試験 数学I・数学A 2014年度 第3問 解説
問題編
問題
$\triangle \mathrm{ ABC }$ は、 $\mathrm{ AB }=4$, $\mathrm{ BC }=2$, $\displaystyle \cos \angle \mathrm{ ABC }=\frac{1}{4}$ を満たすとする。このとき\[ \mathrm{ CA }=[ア],\ \cos\angle \mathrm{ BAC } = \frac{[イ]}{[ウ]}, \ \sin\angle \mathrm{ BAC } = \frac{\sqrt{[エオ]} }{[カ]} \]であり、 $\triangle \mathrm{ ABC }$ の外接円 O の半径は $\displaystyle \frac{[キ]\sqrt{[クケ]} }{[コサ]}$ である。 $\angle \mathrm{ ABC }$ の二等分線と $\angle \mathrm{ BAC }$ の二等分線の交点を D 、直線 BD と辺 AC の交点を E、直線 BD と円 O との交点で B と異なる交点を F とする。
(1) このとき\[ \mathrm{ AE }=\frac{[シ]}{[ス]}, \ \mathrm{ BE }=\frac{[セ]\sqrt{[ソタ]} }{[チ]}, \ \mathrm{ BD } = \frac{[ツ]\sqrt{[テト]} }{[ナ]} \]となる。
(2) $\triangle \mathrm{ EBC }$ の面積は $\triangle \mathrm{ EAF }$ の面積の $\displaystyle \frac{[ニ]}{[ヌ]}$ 倍である。
(3) 角度に注目すると、線分 FA, FC, FD の関係で正しいのは[ネ]であることが分かる。
[ネ]に当てはまるものを、次の0~5のうちから一つ選べ。
0: $\mathrm{ FA }\lt\mathrm{ FC }=\mathrm{ FD }$
1: $\mathrm{ FA }=\mathrm{ FC }\lt\mathrm{ FD }$
2: $\mathrm{ FC }\lt\mathrm{ FA }=\mathrm{ FD }$
3: $\mathrm{ FD }\lt\mathrm{ FC }\lt\mathrm{ FA }$
4: $\mathrm{ FA }=\mathrm{ FC }=\mathrm{ FD }$
5: $\mathrm{ FD }\lt\mathrm{ FC }=\mathrm{ FA }$
考え方
(1)までは、余弦定理・正弦定理を繰り返し使って、考えていきます。角の二等分線の性質も使います。注目する三角形はコロコロ変わるので、視点を変えて考えましょう。
(2)は、相似を使います。(3)はヒントにある通り、角度に注目します。等しい角度がたくさん出てくるので、それを利用して考えます。
解答編
問題
$\triangle \mathrm{ ABC }$ は、 $\mathrm{ AB }=4$, $\mathrm{ BC }=2$, $\displaystyle \cos \angle \mathrm{ ABC }=\frac{1}{4}$ を満たすとする。このとき\[ \mathrm{ CA }=[ア],\ \cos\angle \mathrm{ BAC } = \frac{[イ]}{[ウ]}, \ \sin\angle \mathrm{ BAC } = \frac{\sqrt{[エオ]} }{[カ]} \]であり、 $\triangle \mathrm{ ABC }$ の外接円 O の半径は $\displaystyle \frac{[キ]\sqrt{[クケ]} }{[コサ]}$ である。
解説

余弦定理より、
\begin{eqnarray}
\mathrm{ CA }^2
&=&
4^2+2^2-2\cdot 4\cdot 2 \cdot\frac{1}{4} \\[5pt]
&=&
16+4-4 \\[5pt]
&=&
16 \\[5pt]
\end{eqnarray}なので、 $\mathrm{ CA }=4$ となります。
余弦定理より、
\begin{eqnarray}
\cos\angle \mathrm{ BAC }
&=&
\frac{4^2+4^2-2^2}{2\cdot 4\cdot 4} \\[5pt]
&=&
\frac{28}{32} \\[5pt]
&=&
\frac{7}{8} \\[5pt]
\end{eqnarray}となります。
三角比の相互関係より、
\begin{eqnarray}
\sin\angle \mathrm{ BAC }
&=&
\sqrt{1-\cos^2\angle \mathrm{ BAC } } \\
&=&
\sqrt{1-\frac{7^2}{8^2} } \\[5pt]
&=&
\frac{\sqrt{64-49} }{8} \\[5pt]
&=&
\frac{\sqrt{15} }{8} \\[5pt]
\end{eqnarray}となります。
また、 $\triangle \mathrm{ ABC }$ の外接円の半径を R とすると、正弦定理より
\begin{eqnarray}
R
&=&
\frac{\mathrm{ BC } }{2\sin\mathrm{BAC} } \\[5pt]
&=&
\frac{2}{2\times\frac{\sqrt{15} }{8} } \\[5pt]
&=&
\frac{8}{\sqrt{15} } \\[5pt]
&=&
\frac{8\sqrt{15} }{15} \\[5pt]
\end{eqnarray}となります。
解答
ア:4
イウ:78
エオカ:158
キクケコサ:81515
参考
解答編 つづき
問題
$\angle \mathrm{ ABC }$ の二等分線と $\angle \mathrm{ BAC }$ の二等分線の交点を D 、直線 BD と辺 AC の交点を E、直線 BD と円 O との交点で B と異なる交点を F とする。
(1) このとき\[ \mathrm{ AE }=\frac{[シ]}{[ス]}, \ \mathrm{ BE }=\frac{[セ]\sqrt{[ソタ]} }{[チ]}, \ \mathrm{ BD } = \frac{[ツ]\sqrt{[テト]} }{[ナ]} \]となる。
解説
図を描くと、次のようになっています。
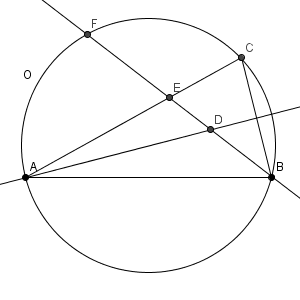
BE は $\angle \mathrm{ ABC }$ の二等分線なので、 $\mathrm{ AB }:\mathrm{ BC }=\mathrm{ AE }:\mathrm{ CE }$ が成り立ちます。このことから、
\begin{eqnarray}
\mathrm{ AE }
&=&
\mathrm{ AC } \times \frac{\mathrm{ AB } }{\mathrm{ AB }+\mathrm{ BC } } \\[5pt]
&=&
4 \times \frac{4}{4+2} \\[5pt]
&=&
\frac{8}{3} \\[5pt]
\end{eqnarray}と求められます。
$\angle\mathrm{ EAB }=\angle\mathrm{ BAC }$ であることを用い、 $\triangle \mathrm{ EAB }$ に対して余弦定理を使うと
\begin{eqnarray}
\mathrm{ BE }^2
&=&
\mathrm{ AB }^2+\mathrm{ AE }^2-2\mathrm{ AB }\cdot \mathrm{ AE }\cdot \cos\angle\mathrm{ EAB } \\[5pt]
&=&
4^2+\frac{8^2}{3^2}-2\cdot 4\cdot \frac{8}{3} \cdot \frac{7}{8} \\[5pt]
&=&
16+\frac{64}{9}-\frac{56}{3} \\[5pt]
&=&
\frac{40}{9} \\[5pt]
\end{eqnarray}と求められます。よって、 $\displaystyle \mathrm{ BE }=\frac{2\sqrt{10} }{3}$ と求められます。
AD は $\angle \mathrm{ BAC }$ の二等分線なので、 $\mathrm{ AB }:\mathrm{ AE }=\mathrm{ BD }:\mathrm{ ED }$ が成り立ちます。このことから、
\begin{eqnarray}
\mathrm{ BD }
&=&
\mathrm{ BE } \times \frac{\mathrm{ AB } }{\mathrm{ AB }+\mathrm{ AE } } \\[5pt]
&=&
\frac{2\sqrt{10} }{3} \times \frac{4}{4+\frac{8}{3} } \\[5pt]
&=&
\frac{2\sqrt{10} }{3} \times \frac{12}{20} \\[5pt]
&=&
\frac{2\sqrt{10} }{5} \\[5pt]
\end{eqnarray}と求められます。
角の二等分線の性質がわかっていないと、解くのは難しいです。また、注目する三角形がコロコロ変わるので、切り替えて考えていきましょう。
解答
シス:83
セソタチ:2103
ツテトナ:2105
参考
解答編 つづき
問題
(2) $\triangle \mathrm{ EBC }$ の面積は $\triangle \mathrm{ EAF }$ の面積の $\displaystyle \frac{[ニ]}{[ヌ]}$ 倍である。
解説

$\triangle \mathrm{ EBC }$ と $\triangle \mathrm{ EAF }$ は相似なので、辺の長さの2乗の比が面積の比になります。
\begin{eqnarray}
\mathrm{ EB }^2:\mathrm{ EA }^2
&=&
\left( \frac{2\sqrt{10} }{3} \right)^2 : \left( \frac{8}{3} \right)^2 \\[5pt]
&=&
\frac{40}{9} : \frac{64}{9} \\[5pt]
&=&
5 : 8 \\[5pt]
\end{eqnarray}なので、$\triangle \mathrm{ EBC }$ の面積は $\triangle \mathrm{ EAF }$ の面積の $\displaystyle \frac{5}{8}$ 倍であることがわかります。
解答
ニヌ:58
解答編 つづき
問題
(3) 角度に注目すると、線分 FA, FC, FD の関係で正しいのは[ネ]であることが分かる。
[ネ]に当てはまるものを、次の0~5のうちから一つ選べ。
0: $\mathrm{ FA }\lt\mathrm{ FC }=\mathrm{ FD }$
1: $\mathrm{ FA }=\mathrm{ FC }\lt\mathrm{ FD }$
2: $\mathrm{ FC }\lt\mathrm{ FA }=\mathrm{ FD }$
3: $\mathrm{ FD }\lt\mathrm{ FC }\lt\mathrm{ FA }$
4: $\mathrm{ FA }=\mathrm{ FC }=\mathrm{ FD }$
5: $\mathrm{ FD }\lt\mathrm{ FC }=\mathrm{ FA }$
解説

BF は $\angle \mathrm{ ABC }$ の二等分線なので、 $\angle \mathrm{ FBA }=\angle \mathrm{ FBC }$ が成り立ちます。また、同じ弧に対する円周角は等しいので、 $\angle \mathrm{ FBA }=\angle \mathrm{ FCA }$, $\angle \mathrm{ FBC }=\angle \mathrm{ FAC }$ が成り立ちます。以上から、 $\angle \mathrm{ FCA }=\angle \mathrm{ FAC }$ が成り立つので、 $\mathrm{ FC }=\mathrm{ FA }$ が成り立ちます。
また、 $\angle \mathrm{ FDA }=\angle \mathrm{ DAB }+\angle \mathrm{ DBA }$ であり、 $\angle \mathrm{ DAB }=\angle \mathrm{ EAD }$ と $\angle \mathrm{ DBA }=\angle \mathrm{ FCA }=\angle \mathrm{ FAE }$ より、 $\angle \mathrm{ FDA }=\angle \mathrm{ FAC }$ となります。よって、 $\mathrm{ FA }=\mathrm{ FD }$ が成り立ちます。
最後は、特に三角比を使わずに解くことができます。





