センター試験 数学I・数学A 2014年度 第2問 解説
問題編
問題
a を定数とし、 x の2次関数\[ y=x^2+2ax+3a^2-6a-36 \quad\cdots ① \]のグラフを G とする。 G の頂点の座標は\[ ([ア]a,[イ]a^2-[ウ]a-[エオ]) \]である。 G と y 軸との交点の y 座標を p とする。
(1) $p=-27$ のとき、 a の値は $a=[カ],[キク]$ である。 $a=[カ]$ のときの①のグラフを x 軸方向に [ケ]、 y 軸方向に[コ]だけ平行移動すると、 $a=[キク]$ のときの①のグラフに一致する。
(2) 下の[ス]、[セ]、[ノ]、[ハ]には、次の 0 ~ 3 のうちから当てはまるものを一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $\gt\ $ 1: $\lt\ $ 2: $\geqq\ $ 3: $\leqq$G が x 軸と共有点を持つような a の値の範囲を表す不等式は\[ [サシ][ス]a[セ][ソ] \quad\cdots ② \]である。 a が②の範囲にあるとき、 p は $a=[タ]$ で最小値[チツテ]をとり、 $a=[ト]$ で最大値[ナニ]をとる。
G が x 軸と共有点を持ち、さらにそのすべての共有点の x 座標が $-1$ より大きくなるような a の値の範囲を表す不等式は\[ [ヌネ][ノ]a[ハ]\frac{[ヒフ]}{[ヘ]} \]である。
考え方
(1)の後半部分は、事前に求めた頂点の座標を使って考えましょう。
(2)の後半は、グラフがどうなっていれば求める条件を満たすか、を考えます。軸や $x=-1$ での y 座標で考えます。選択肢はイコールのあるなしも考えないといけないので、「イコールのときに条件を満たすかどうか」に注意して解いていきましょう。
解答編
問題
a を定数とし、 x の2次関数\[ y=x^2+2ax+3a^2-6a-36 \quad\cdots ① \]のグラフを G とする。 G の頂点の座標は\[ ([ア]a,[イ]a^2-[ウ]a-[エオ]) \]である。 G と y 軸との交点の y 座標を p とする。
解説
頂点を求めるためには、平方完成を行えばいいですね。
\begin{eqnarray}
y
&=&
x^2+2ax+3a^2-6a-36 \\
&=&
(x+a)^2-a^2+3a^2-6a-36 \\
&=&
(x+a)^2+2a^2-6a-36 \\
\end{eqnarray}これから、頂点の座標は\[ (-a,2a^2-6a-36) \]となることがわかります。
解答
アイウエオ:-2636
参考
解答編 つづき
問題
(1) $p=-27$ のとき、 a の値は $a=[カ],[キク]$ である。
解説
$p=-27$ なので、 $3a^2-6a-36=-27$ という方程式を解けばいいですね。
\begin{eqnarray}
3a^2-6a-36 &=& -27 \\
3a^2-6a-9 &=& 0 \\
a^2-2a-3 &=& 0 \\
(a-3)(a+1) &=& 0 \\
\end{eqnarray}なので、 $a=3,-1$ と求められます。
解答
カキク:3-1
解答編 つづき
問題
$a=[カ]$ のときの①のグラフを x 軸方向に [ケ]、 y 軸方向に[コ]だけ平行移動すると、 $a=[キク]$ のときの①のグラフに一致する。
解説
はじめに G の頂点の座標を求めていたので、これを利用してグラフがどう移動すればいいかを考えましょう。
$a=3$ のときの頂点は
\begin{eqnarray}
& &
(-a,2a^2-6a-36) \\
&=&
(-3,2\cdot9-6\cdot3-36) \\
&=&
(-3,-36) \\
\end{eqnarray}となります。 $a=-1$ のときの頂点は
\begin{eqnarray}
& &
(-a,2a^2-6a-36) \\
&=&
(1,2\cdot(-1)^2-6\cdot(-1)-36) \\
&=&
(1,-28) \\
\end{eqnarray}となります。 $(-3,-36)$ が $(1,-28)$ に移るためには、 x 軸方向に $1-(-3)=4$ だけ移動し、 y 軸方向に $-28-(-36)=8$ だけ移動すればいいですね。 $x^2$ の係数が同じなので、頂点が一致するように平行移動すれば、グラフ全体が一致するようになります。
解答
ケコ:48
解答編 つづき
問題
(2) 下の[ス]、[セ]、[ノ]、[ハ]には、次の 0 ~ 3 のうちから当てはまるものを一つずつ選べ。ただし、同じものを繰り返し選んでもよい。
0: $\gt\ $ 1: $\lt\ $ 2: $\geqq\ $ 3: $\leqq$G が x 軸と共有点を持つような a の値の範囲を表す不等式は\[ [サシ][ス]a[セ][ソ] \quad\cdots ② \]である。
解説
G が x 軸と共有点を持つ、というのは、「判別式が0以上」と考えてもいいんですが、はじめに頂点の座標を求めているので、それを使った方がいいでしょう。 G は下に凸の放物線なので、 x 軸と共有点を持つためには、頂点の y 座標が0以下であればいいですね。0でもいいので、イコールが入ります。
\begin{eqnarray}
2a^2-6a-36 & \leqq & 0 \\
a^2-3a-18 & \leqq & 0 \\
(a-6)(a+3) & \leqq & 0 \\
\end{eqnarray}$y=(a-6)(a+3)$ のグラフは下の通りなので、求める範囲は $-3\leqq a \leqq 6$ となります。
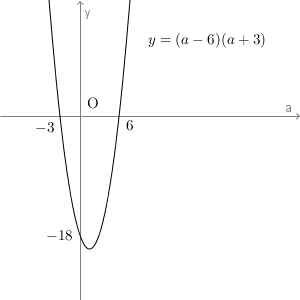
解答
サシス:-33
セソ:36
解答編 つづき
問題
a が②の範囲にあるとき、 p は $a=[タ]$ で最小値[チツテ]をとり、 $a=[ト]$ で最大値[ナニ]をとる。
解説
$p=3a^2-6a-36$ なので、 $-3\leqq a \leqq 6$ の範囲でこの二次関数の最大・最小を考えればいいですね。
\begin{eqnarray}
p
&=&
3a^2-6a-36 \\
&=&
3(a^2-2a)-36 \\
&=&
3(a-1)^2-3-36 \\
&=&
3(a-1)^2-39 \\
\end{eqnarray}このグラフをかくと、次のようになります。
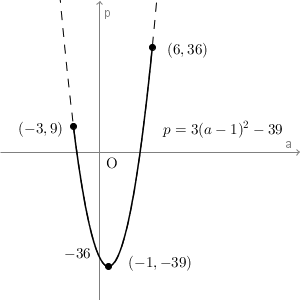
これから、 $a=1$ のときに最小値 $-39$ をとることがわかります。また、 $a=6$ のときに最大値 $36$ をとることもわかります。
解答
タチツテ:1-39
トナニ:636
参考
解答編 つづき
問題
G が x 軸と共有点を持ち、さらにそのすべての共有点の x 座標が $-1$ より大きくなるような a の値の範囲を表す不等式は\[ [ヌネ][ノ]a[ハ]\frac{[ヒフ]}{[ヘ]} \]である。
解説
G が x 軸と共有点を持つ条件は、先ほど求めた通り、 $-3\leqq a \leqq 6$ です。
すべての共有点の x 座標が $-1$ より大きくなる、ということは、「 $G$ の軸が $x=-1$ より右にあり、 $x=-1$ のときの y 座標が正である」ということと同値です。なので、この条件を求めます。
頂点の x 座標は、はじめに求めた通り $-a$ なので、「 $G$ の軸が $x=-1$ より右にある」というのは、 $-a\gt -1$ 、つまり、 $a\lt 1$ ということです。軸が $x=-1$ のときは、条件を満たさないので、イコールは入りません。
また、 $x=-1$ のときの y 座標が正になるのは
\begin{eqnarray}
(-1)^2+2a\cdot(-1)+3a^2-6a-36 \gt 0 \\
3a^2-8a-35 \gt 0 \\
(3a+7)(a-5) \gt 0 \\
\end{eqnarray}なので、下のグラフから $\displaystyle a\lt -\frac{7}{3}, a\gt 5$ と求められます。これも、イコールは入りません。
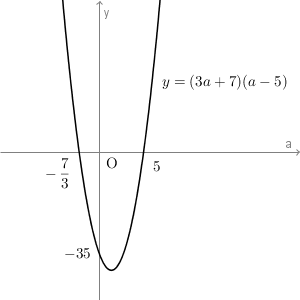
以上から、求める範囲は次の3つの範囲の共通部分となります。
A: $-3\leqq a \leqq 6$
B: $a\lt 1$
C: $\displaystyle a\lt -\frac{7}{3}, a\gt 5$
数直線で考えると、次のようになります。
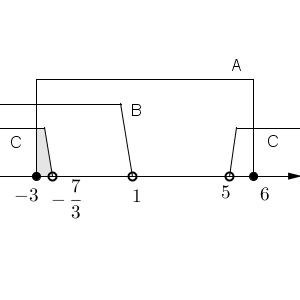
これより、 $\displaystyle -3\leqq a \leqq -\frac{7}{3}$ が求める範囲となります。
解答
ヌネノ:-33
ハヒフ:1-73





