センター試験 数学I・数学A 2006年度 第2問 解説
問題編
【問題】
2次関数\[ y=6x^2+11x-10 \quad \cdots ① \]について考える。①において、$y\leqq 0$となるxの範囲は\[ \frac{[アイ]}{[ウ]} \leqq x \leqq \frac{[エ]}{[オ]} \]である。
①のグラフをx軸方向にa、y軸方向にbだけ平行移動して得られるグラフをGとする。Gが原点$(0,0)$を通るとき、\[ b=[カキ]a^2+[クケ]a+[コサ] \]であり、このときGを表す2次関数は\[ y = [シ]x^2 -([スセ]a-[ソタ])x \quad \cdots ② \]である。
$x=-2$と$x=3$に対応する2次関数②の値が等しくなるのは\[ a=\frac{[チツ]}{[テト]} \]のときである。このとき、2次関数②の$-2\leqq x\leqq 3$における
最小値は$\displaystyle \frac{[ナニ]}{[ヌ]}$、最大値は[ネノ]
である。
【考え方】
1つ目は、因数分解をしてグラフを描けばわかります。
その次は、平行移動した後のグラフに関する問題です。xの部分に$x-a$を、yの部分に$y-b$を代入すれば、移動後のグラフを表す式になります。これに「グラフが原点を通る」という条件を考えれば、解くことができます。
後半は、$x=-2$と$x=3$を代入した値が等しくなる、ということですね。下に凸で両端の値が等しくなるので、この区間での最小値は頂点、最大値は区間の端になります。
解答編
【問題】
2次関数\[ y=6x^2+11x-10 \quad \cdots ① \]について考える。①において、$y\leqq 0$となるxの範囲は\[ \frac{[アイ]}{[ウ]} \leqq x \leqq \frac{[エ]}{[オ]} \]である。
【解説】
\begin{eqnarray}
6x^2+11x-10
&=&
(3x-2)(2x+5)
\end{eqnarray}なので、グラフは次のようになります。
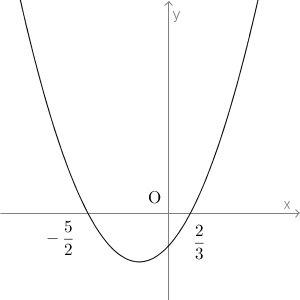
よって、$y\leqq 0$となる範囲は、\[ -\frac{5}{2} \leqq x \leqq \frac{2}{3} \]となります。
【解答】
アイウ:-52
エオ:23
【問題】
①のグラフをx軸方向にa、y軸方向にbだけ平行移動して得られるグラフをGとする。Gが原点$(0,0)$を通るとき、\[ b=[カキ]a^2+[クケ]a+[コサ] \]であり、このときGを表す2次関数は\[ y = [シ]x^2 -([スセ]a-[ソタ])x \quad \cdots ② \]である。
【解説】
平行移動した後のグラフを表す関数は、①で、xに$x-a$を、yに$y-b$を代入すれば求められるので、
\begin{eqnarray}
y-b &=& 6(x-a)^2+11(x-a)-10
\end{eqnarray}となります。
これが原点を通るので、
\begin{eqnarray}
0-b &=& 6(0-a)^2+11(0-a)-10
\end{eqnarray}が成り立ちます。これを変形していけば、
\begin{eqnarray}
-b &=& 6a^2-11a-10 \\
b &=& -6a^2+11a+10 \\
\end{eqnarray}となることがわかります。これをもとの式に代入すると
\begin{eqnarray}
y &=& 6(x-a)^2+11(x-a)-10 + (-6a^2+11a+10) \\
y &=& 6x^2-12ax+6a^2 \\
& & +11x-11a-10 -6a^2+11a+10 \\
y &=& 6x^2-12ax+11x \\
y &=& 6x^2-(12a-11)x
\end{eqnarray}となります。
【解答】
カキクケコサ:-61110
シスセソタ:61211
【問題】
$x=-2$と$x=3$に対応する2次関数②の値が等しくなるのは\[ a=\frac{[チツ]}{[テト]} \]のときである。
【解説】
②は、$y = 6x^2-(12a-11)x$なので、$x=-2$のときと$x=3$のときが等しいとすると、
\begin{eqnarray}
6(-2)^2-(12a-11)\times (-2)
&=&
6\cdot 3^2-(12a-11)\times 3
\\
24+24a-22
&=&
54-36a+33
\\
60a &=& 85
\\
a &=& \frac{17}{12}
\end{eqnarray}となります。
【解答】
チツテト:1712
【問題】
このとき、2次関数②の$-2\leqq x\leqq 3$における
最小値は$\displaystyle \frac{[ナニ]}{[ヌ]}$、最大値は[ネノ]
である。
【解説】
②の式$y = 6x^2-(12a-11)x$に先ほどの解答$\displaystyle a=\frac{17}{12}$を代入すると、\[ y=6x^2-6x \]が得られます。
【解答】
ナニヌ:-12
ネノ:32





