【標準】三角比と直方体
ここでは、直方体の断面が三角形になるときに、断面の面積を求める問題を考えてみます。また、頂点から断面に下した垂線の長さも求めてみます。
例題
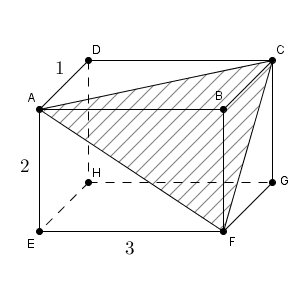
三角形 ACF の3辺の長さはすぐに出せます。3辺の長さがわかれば、三角形の面積は出せますね。【標準】三角比と三角形の面積でやったやり方が使えます。
まずは、3辺の長さを求めましょう。三平方の定理から
\begin{eqnarray}
& & \mathrm{ AC }^2=3^2+1^2=10\\
& & \mathrm{ CF }^2=1^2+2^2=5 \\
& & \mathrm{ FA }^2=2^2+3^2=13 \\
\end{eqnarray}と求められます。余弦定理から
\begin{eqnarray}
\cos \angle \mathrm{ ACF }
&=&
\frac{10+5-13}{2\cdot\sqrt{10}\cdot\sqrt{5} } \\[5pt]
&=&
\frac{2}{2\cdot\sqrt{10}\cdot\sqrt{5} } \\[5pt]
&=&
\frac{1}{\sqrt{50} } \\[5pt]
\end{eqnarray}となります。三角比の相互関係から
\begin{eqnarray}
\sin \angle \mathrm{ ACF }
&=&
\sqrt{ 1-\left(\frac{1}{\sqrt{50} }\right)^2 } \\[5pt]
&=&
\frac{\sqrt{50-1} }{\sqrt{50} } \\[5pt]
&=&
\frac{7}{\sqrt{50} } \\[5pt]
\end{eqnarray}と求められるので、三角形 ACF の面積は
\begin{eqnarray}
& &
\frac{1}{2}\times \mathrm{ AC }\times\mathrm{ CF }\times \sin \angle \mathrm{ ACF } \\[5pt]
&=&
\frac{1}{2}\times \sqrt{10}\times\sqrt{5}\times \frac{7}{\sqrt{50} } \\[5pt]
&=&
\frac{7}{2}
\end{eqnarray}と求めることができます。
垂線の長さ
上の例題で、点 B から三角形 ACF に下した垂線の長さを求めさせる問題もよく出題されます。これは、四面体 BACF の体積を2通りに表すことで求めることができます。

四面体 BACF の底面を三角形 BCF だと考えれば、この四面体の体積は次のように書くことができます。\[ \frac{1}{3}\times \mathrm{ AB }\times\frac{1}{2}\times \mathrm{ BC }\times \mathrm{ BF }=1 \]一方、三角形 ACF が底面だと考えてみましょう。垂線の高さを h とすれば、さきほど求めた三角形 ACF の面積から、この四面体の体積は次のように書けます。\[ \frac{1}{3}\times h \times \frac{7}{2}=\frac{7h}{6} \]どちらの方法で求めても体積は同じなので、このことから\[ h=\frac{6}{7} \]と求めることができます。
このように、四面体の体積を2通りに表して、垂線の長さを求める問題もよく出題されます。
おわりに
ここでは、直方体の断面が三角形のときに、断面の面積を求める問題を考えました。3辺の長さから三角形の面積を求める、という流れに帰着させて考えて解くことができます。また、頂点から断面に下した垂線の長さの求め方も見ました。四面体の体積に着目して解く方法は、三角比の分野に限らずいろんなところで使うので慣れておきましょう。





