【基本】三角形の重心の位置ベクトル

ここでは、内分点の位置ベクトルを使って、三角形の重心の位置ベクトルについて見ていきます。

三角形の重心の復習

三角形の重心の位置ベクトルを考える前に、まずは三角形の重心とは何だったか、どのような点だったかを復習しておきましょう。

【基本】三角形の重心でも見た通り、三角形の重心とは、3つの中線の交点です。中線とは、頂点と、対辺の中点とを結んでできる線分のことです。

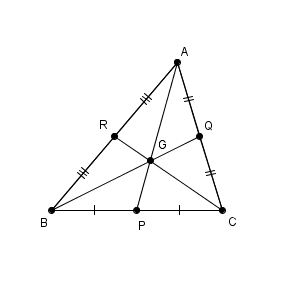
上の図で、 AP などが中線です。そして、 G がこの三角形 ABC の重心です。

重心は、中線を $2:1$ に内分します。つまり、 $\mathrm{ AG }:\mathrm{ GP }=2:1$ などが成り立つ、ということです。これも、上のリンク先で見た内容です。

これらのことから、重心の位置ベクトルを求めるために、まず中点の位置ベクトルを考え、その次に中線の内分点を考える、という順番で進めていきます。

中点の位置ベクトル

三角形 ABC の重心の位置ベクトルを求めるため、まずは BC の中点 P の位置ベクトルを求めましょう。

$\mathrm{ A }(\vec{a})$, $\mathrm{ B }(\vec{b})$, $\mathrm{ C }(\vec{c})$ と位置ベクトルを定め、 P の位置ベクトル $\vec{p}$ について考えましょう。

P は、 BC を $1:1$ に内分する点なので、【基本】内分点と外分点の位置ベクトルで見た内容から、\[ \vec{p}=\frac{\vec{b}+\vec{c} }{2} \]となります。

足して2で割ったものが中点の位置ベクトルになるんですね。覚えやすいですね。

三角形の重心の位置ベクトル

さて、続いて、重心の位置ベクトルを $\vec{g}$ とおいて、これについて考えましょう。

重心 G は、 AP を $2:1$ に内分します。再び、上で見た内分点の式から
\begin{eqnarray} \vec{g} &=& \frac{\vec{a}+2\vec{p} }{2+1} \\[5pt] &=& \frac{\vec{a}+2\times\dfrac{\vec{b}+\vec{c} }{2} }{3} \\[5pt] &=& \frac{\vec{a}+\vec{b}+\vec{c} }{3} \\[5pt] \end{eqnarray}となります。3つの頂点の位置ベクトルを足して3で割ったものが重心の位置ベクトルになるんですね。これも覚えやすいですね。

ここでは、 AP から考えましたが、 BQ から考えても CR から考えても、同じ結果にたどりつきます。

他の分野との比較

三角形の重心については、他の分野でも扱いました。これらとの比較をしてみましょう。

まずは、座標を使ったものと比較してみましょう。【標準】三角形の重心の座標で出てきた通り、重心の座標は、各頂点の座標について、 x 座標と y 座標をそれぞれ足して3で割って求めます。ベクトルでの式と似ていますが、ベクトルで書くと1つにまとめられるのでスッキリしますね。

実は、ベクトルの分野でも、【標準】三角形とベクトルの演算で、重心のベクトルについて考えています。このときは\[ \overrightarrow{ \mathrm{ AG } }=\frac{\overrightarrow{ \mathrm{ AB } } + \overrightarrow{ \mathrm{ AC } } }{3} \]という式になっています。これは上で見た式と違いますが、原因は基準点の違いです。リンク先では A を基準としていたため $\vec{a}$ が隠れていますが、実際には上のように位置ベクトルで考えたほうがきれいになります。3頂点の位置ベクトルを足して3で割る、となりますからね。重心のベクトルは、位置ベクトルを使って書くようにすると考えやすくなるでしょう。

おわりに

ここでは、三角形の重心の位置ベクトルを見てきました。内分点の位置ベクトルを使って考えることができます。中点は足して2で割る、重心は足して3で割る、というのは、覚えやすい結果ですね。