京都大学理系 2017年度第4問解説

🕒 2017/02/25 🔄 2023/05/01

問題編

問題

　$\triangle \mathrm{ ABC }$ は鋭角三角形であり、 $\angle \mathrm{ A }=\dfrac{\pi}{3}$ であるとする。また $\triangle \mathrm{ ABC }$ の外接円の半径は $1$ であるとする。
(1) $\triangle \mathrm{ ABC }$ の内心を P とするとき、 $\angle \mathrm{ BPC }$ を求めよ。
(2) $\triangle \mathrm{ ABC }$ の内接円の半径 r の取りうる値の範囲を求めよ。

考え方

(1)は図形の問題として考えます。内心から各辺に垂線をおろし、いくつかの三角形に分割して考えれば求めやすくなります。

(2)も、図形の性質をよく使うと、それほど計算は必要ありません。(1)から P がどういう点なのかがわかるので、それを利用して解きましょう。

解答編

問題

　$\triangle \mathrm{ ABC }$ は鋭角三角形であり、 $\angle \mathrm{ A }=\dfrac{\pi}{3}$ であるとする。また $\triangle \mathrm{ ABC }$ の外接円の半径は $1$ であるとする。
(1) $\triangle \mathrm{ ABC }$ の内心を P とするとき、 $\angle \mathrm{ BPC }$ を求めよ。
(2) $\triangle \mathrm{ ABC }$ の内接円の半径 r の取りうる値の範囲を求めよ。

解答

(1)
P から AB, BC, CA に下した垂線の足を、それぞれ Q, R, S とする。

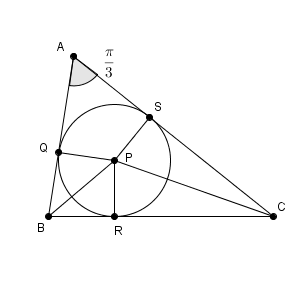
このとき、四角形 AQPS の内角の和は $2\pi$ なので\[ \angle \mathrm{ QPS }=2\pi-\frac{\pi}{3}-\frac{\pi}{2}-\frac{\pi}{2}=\frac{2\pi}{3} \]となる。また、三角形PQBと三角形PRBは合同で、三角形PSCと三角形PRCが合同なので、\[ \angle \mathrm{ BPC }=\frac{2\pi-\angle \mathrm{ QPS } }{2}=\frac{2}{3}\pi \]となる。

(2)
正弦定理から\[ \mathrm{ BC }=2\times 1 \times\sin \angle \mathrm{ A }=\sqrt{3} \]となる。(1)より、BC を固定して条件を満たすように A を動かした場合、 P は B, C を通る、ある円の円周上を動く。

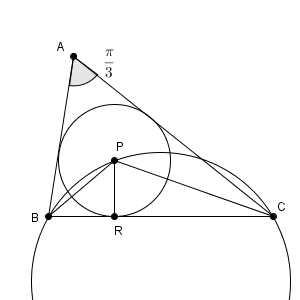
よって、内接円の半径が最大となるのは、P が BC の垂直二等分線上にあるときであり、そのとき三角形 PBC は二等辺三角形になる。よって、このときの r は\[ r=\frac{\mathrm{ BR } }{\tan \frac{\pi}{3} }=\frac{1}{2} \]となる。

対称性より、 $\angle \mathrm{ B } \geqq \angle \mathrm{ C }$ の場合を考えればよい。このとき、 $\angle \mathrm{ B }$ が大きくなるにつれて、内接円の半径は連続的に小さくなる。ここで、 $\angle \mathrm{ B }=\dfrac{1}{2}\pi$ のときの内接円の半径を求める。

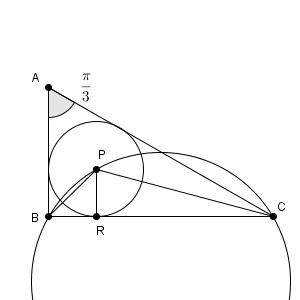
三角形 ABC の面積に着目して
\begin{eqnarray} \frac{1}{2}\times 1\times \sqrt{3} &=& \frac{1}{2}\times r(1+2+\sqrt{3}) \\[5pt] r &=& \frac{\sqrt{3} }{3+\sqrt{3} } \\[5pt] &=& \frac{\sqrt{3}(3-\sqrt{3})}{6} \\[5pt] &=& \frac{\sqrt{3}-1}{2} \\[5pt] \end{eqnarray}となる。