京都大学理系 2017年度第2問解説

🕒 2017/02/26 🔄 2023/05/01

問題編

問題

　四面体 OABC を考える。点 D, E, F, G, H, I は、それぞれ辺 OA, AB, BC, CO, OB, AC 上にあり、頂点ではないとする。このとき、次の問に答えよ。

(1) $\overrightarrow{ \mathrm{ DG } }$ と $\overrightarrow{ \mathrm{ EF } }$ が平行ならば $\mathrm{ AE }:\mathrm{ EB } = \mathrm{ CF }:\mathrm{ FB }$ であることを示せ。
(2) D, E, F, G, H, I が正八面体の頂点となっているとき、これらの点は OABC の各辺の中点であり、 OABC は正四面体であることを示せ。

考え方

(1)はベクトルを使って考えます。条件をベクトルで表現して考えましょう。

(2)は(1)を使うのが見え見えです。対称性から(1)を複数回使って、正八面体の各頂点のどれか1つが四面体の辺の中点になることを示しましょう。1つ示せれば、他は同様です。また、正四面体であることを示すには、正八面体の辺の長さと四面体の辺の長さの関係に注目しましょう。

解答編

問題

　四面体 OABC を考える。点 D, E, F, G, H, I は、それぞれ辺 OA, AB, BC, CO, OB, AC 上にあり、頂点ではないとする。このとき、次の問に答えよ。

(1) $\overrightarrow{ \mathrm{ DG } }$ と $\overrightarrow{ \mathrm{ EF } }$ が平行ならば $\mathrm{ AE }:\mathrm{ EB } = \mathrm{ CF }:\mathrm{ FB }$ であることを示せ。
(2) D, E, F, G, H, I が正八面体の頂点となっているとき、これらの点は OABC の各辺の中点であり、 OABC は正四面体であることを示せ。

解答

(1)
$\overrightarrow{ \mathrm{ OA } }=\overrightarrow{ a }$, $\overrightarrow{ \mathrm{ OB } }=\overrightarrow{ b }$, $\overrightarrow{ \mathrm{ OC } }=\overrightarrow{ c }$ とする。

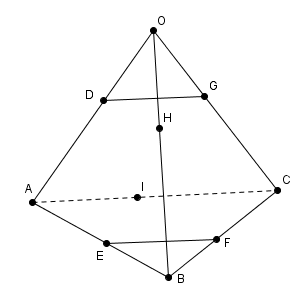
$\mathrm{ OD }:\mathrm{ DA } = d:(1-d)$ とすると、 $\overrightarrow{ \mathrm{ OD } } = d\overrightarrow{ a }$ となる。
$\mathrm{ OG }:\mathrm{ GC } = g:(1-g)$ とすると、 $\overrightarrow{ \mathrm{ OG } } = g\overrightarrow{ c }$ となる。

$\mathrm{ BE }:\mathrm{ EA } = e:(1-e)$ とすると、 $\overrightarrow{ \mathrm{ OE } } = e\overrightarrow{ a }+(1-e)\overrightarrow{ b }$ となる。
$\mathrm{ BF }:\mathrm{ FC } = f:(1-f)$ とすると、 $\overrightarrow{ \mathrm{ OF } } = f\overrightarrow{ c }+(1-f)\overrightarrow{ b }$ となる。

以上から、
\begin{eqnarray} \overrightarrow{ \mathrm{ DG } } &=& g\overrightarrow{ c }-d\overrightarrow{ a } \\ \overrightarrow{ \mathrm{ EF } } &=& f\overrightarrow{ c }+(1-f)\overrightarrow{ b }-e\overrightarrow{ a }-(1-e)\overrightarrow{ b } \\ \end{eqnarray}となる。

ここで、 $\overrightarrow{ \mathrm{ DG } }$ と $\overrightarrow{ \mathrm{ EF } }$ が平行であること、 O, A, B, C が同一平面上にないこと、上の1つ目の式の $\overrightarrow{ b }$ の係数が0であることから、2つ目の式の $\overrightarrow{ b }$ の係数も0であることがわかる。よって
\begin{eqnarray} 1-f-(1-e) &=& 0 \\ e &=& f \\ \end{eqnarray}が得られる。もともと、$\mathrm{ BE }:\mathrm{ EA } = e:(1-e)$, $\mathrm{ BF }:\mathrm{ FC } = f:(1-f)$ とおいていたので、 $e=f$ から\[ \mathrm{ AE }:\mathrm{ EB } = \mathrm{ CF }:\mathrm{ FB } \]となることがわかる。

(2)
D, E, F, G, H, I が正八面体の頂点となっているとき、 $\overrightarrow{ \mathrm{ DG } }$ と $\overrightarrow{ \mathrm{ EF } }$ は平行なので、(1)より\[ \mathrm{ AE }:\mathrm{ EB } = \mathrm{ CF }:\mathrm{ FB } \]である。

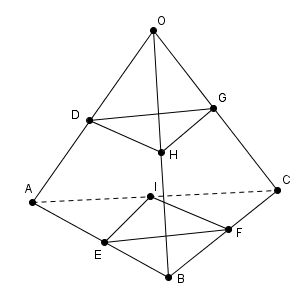
また、 $\overrightarrow{ \mathrm{ HG } }$ と $\overrightarrow{ \mathrm{ EI } }$ は平行なので、(1)と同様の議論により、\[ \mathrm{ BE }:\mathrm{ EA } = \mathrm{ CI }:\mathrm{ IA } \]が得られる。さらに、 $\overrightarrow{ \mathrm{ DH } }$ と $\overrightarrow{ \mathrm{ IF } }$ は平行なので、(1)と同様の議論により、 \[ \mathrm{ AI }:\mathrm{ IC } = \mathrm{ BF }:\mathrm{ FC } \]が得られる。

以上から
\begin{eqnarray} \mathrm{ AI }:\mathrm{ IC } &=& \mathrm{ BF }:\mathrm{ FC } \quad (3つ目) \\ &=& \mathrm{ BE }:\mathrm{ EA } \quad (1つ目) \\ &=& \mathrm{ CI }:\mathrm{ IA } \quad (2つ目) \\ \end{eqnarray}となり、$\mathrm{ AI }^2 = \mathrm{ IC }^2$ が得られるので、これから I は AC の中点であることがわかる。

対称性から、正八面体の他の頂点についても、四面体の各辺の中点であることがわかる。

また、中点連結定理から、 $\mathrm{ AB }=2\mathrm{ DH }$ がわかる。このことから、四面体の他の辺についても、辺の長さが正八面体の一辺の長さの2倍であることがわかるため、四面体の各面は正三角形であることがわかる。よって、四面体 OABC は正四面体となる。

（終）