京都大学理系 2017年度第1問解説

🕒 2017/02/26 🔄 2023/05/01

問題編

問題

　w を0でない複素数、 x, y を $w+\dfrac{1}{w}=x+yi$ を満たす実数とする。

(1) 実数 R は $R\gt 1$ を満たす定数とする。 w が絶対値 R の複素数全体を動くとき、 xy 平面上の点 $(x,y)$ の軌跡を求めよ。
(2) 実数 $\alpha$ は $0\lt \alpha\lt \dfrac{\pi}{2}$ を満たす定数とする。 w が偏角 $\alpha$ の複素数全体を動くとき、 xy 平面上の点 $(x,y)$ の軌跡を求めよ。

考え方

まずは、実部・虚部を比較して式を作りましょう。そのあとは、(1)は偏角が消えるように、(2)は絶対値が消えるように変形していきます。

解答編

問題

　w を0でない複素数、 x, y を $w+\dfrac{1}{w}=x+yi$ を満たす実数とする。

(1) 実数 R は $R\gt 1$ を満たす定数とする。 w が絶対値 R の複素数全体を動くとき、 xy 平面上の点 $(x,y)$ の軌跡を求めよ。
(2) 実数 $\alpha$ は $0\lt \alpha\lt \dfrac{\pi}{2}$ を満たす定数とする。 w が偏角 $\alpha$ の複素数全体を動くとき、 xy 平面上の点 $(x,y)$ の軌跡を求めよ。

解答

(1)
$w=R(\cos\theta+i\sin\theta)$ とおける（ $0\leqq\theta\lt 2\pi$ ）。このとき
\begin{eqnarray} w+\frac{1}{w} &=& R(\cos\theta+i\sin\theta) +\frac{1}{R}(\cos\theta-i\sin\theta) \\[5pt] &=& \left(R+\frac{1}{R}\right)\cos\theta +i\left(R-\frac{1}{R}\right)\sin\theta \\[5pt] \end{eqnarray}となるので \begin{eqnarray} x &=& \left(R+\frac{1}{R}\right)\cos\theta \\[5pt] y &=& \left(R-\frac{1}{R}\right)\sin\theta \\[5pt] \end{eqnarray}となる。この2つの式を A とおく。

ここで、 $R\gt 1$ より、 $R+\dfrac{1}{R}\gt 0$, $R-\dfrac{1}{R}\gt 0$ が成り立つ。また、 $\cos^2 \theta +\sin^2\theta=1$ が成り立つので、
\begin{eqnarray} \left(\frac{x}{R+\frac{1}{R} }\right)^2 +\left(\frac{y}{R-\frac{1}{R} }\right)^2 &=& 1 \end{eqnarray}が成り立つ。逆に、これを満たす $(x,y)$ に対して、 A を満たす $\theta$ は必ず存在するので、対応する w が存在することもわかる。

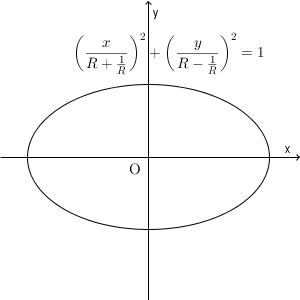
よって、求める軌跡は、楕円\[ \left(\frac{x}{R+\frac{1}{R} }\right)^2 +\left(\frac{y}{R-\frac{1}{R} }\right)^2 = 1 \]である。

(2)
$w=r(\cos\theta+i\sin\theta)$ とおける（ $r\gt 0$ ）。このとき、(1)と同様にして
\begin{eqnarray} x &=& \left(r+\frac{1}{r}\right)\cos\alpha \\[5pt] y &=& \left(r-\frac{1}{r}\right)\sin\alpha \\[5pt] \end{eqnarray}が得られる。この2つの式を B とおく。

ここで、 $0\lt \alpha\lt \dfrac{\pi}{2}$ だから、 $\cos\alpha \ne 0$, $\sin\alpha \ne 0$ となる。よって、
\begin{eqnarray} r+\frac{1}{r} &=& \frac{x}{\cos\alpha} \\[5pt] r-\frac{1}{r} &=& \frac{y}{\sin\alpha} \\[5pt] \end{eqnarray}が得られる。この2つの式を辺々足したものと、辺々引いたものから \begin{eqnarray} r &=& \frac{1}{2} \left(\frac{x}{\cos\alpha}+\frac{y}{\sin\alpha}\right) \\[5pt] \frac{1}{r} &=& \frac{1}{2} \left(\frac{x}{\cos\alpha}-\frac{y}{\sin\alpha}\right) \\[5pt] \end{eqnarray}が得られる。この2つの式を辺々掛け合わせると \begin{eqnarray} 1 &=& \frac{1}{4}\left(\frac{x}{\cos\alpha}+\frac{y}{\sin\alpha}\right)\left(\frac{x}{\cos\alpha}-\frac{y}{\sin\alpha}\right) \\[5pt] \end{eqnarray}から \begin{eqnarray} \left(\frac{x}{2\cos\alpha}\right)^2-\left(\frac{y}{2\sin\alpha}\right)^2 &=& 1 \end{eqnarray}が得られる。ここで、 $r\gt 0$ より\[ \frac{x}{\cos\alpha}+\frac{y}{\sin\alpha} \gt 0 \]も満たす必要がある。
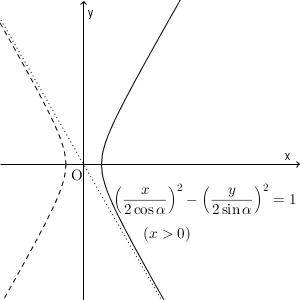
これは、グラフから、 $x\gt 0$ の部分であることがわかる。