京都大学 理系 2014年度 第6問 解説
問題編
問題
双曲線 $y=\dfrac{1}{x}$ の第1象限にある部分と、原点 O を中心とする円の第1象限にある部分を、それぞれ $C_1$, $C_2$ とする。 $C_1$ と $C_2$ は2つの異なる点 A, B で交わり、点 A における $C_1$ の接線 l と線分 OA のなす角は $\dfrac{\pi}{6}$ であるとする。このとき、 $C_1$ と $C_2$ で囲まれる図形の面積を求めよ。
考え方
面積を求めるためには、まず円の半径がいくらかを求めなければいけません。いろいろ求め方はありますが、半径を求めること自体はそれほど難しくはないでしょう。点 A の座標も、その過程で求められます。
半径がわかればあとは積分するだけですが、そのまま積分するのは大変です。図形的な性質を使えば、計算を省略することができます。
解答編
問題
双曲線 $y=\dfrac{1}{x}$ の第1象限にある部分と、原点 O を中心とする円の第1象限にある部分を、それぞれ $C_1$, $C_2$ とする。 $C_1$ と $C_2$ は2つの異なる点 A, B で交わり、点 A における $C_1$ の接線 l と線分 OA のなす角は $\dfrac{\pi}{6}$ であるとする。このとき、 $C_1$ と $C_2$ で囲まれる図形の面積を求めよ。
解答
図形は直線 $y=x$ に関して対称なので、 A の y 座標は x 座標以上としてよい。また、接線 l と x 軸との交点を D とする。
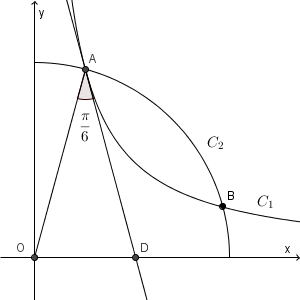
点 A の x 座標を a とすると、 A は $C_1$ 上の点なので、座標は $\left(a,\dfrac{1}{a}\right)$ とかける。また、 $y=\dfrac{1}{x}$ の両辺を微分すると $y'=-\dfrac{1}{x^2}$ なので、接線 l の方程式は
\begin{eqnarray}
y -\frac{1}{a} &=& -\frac{1}{a^2} \left(x-a\right) \\[5pt]
y &=& -\frac{1}{a^2}x +\frac{2}{a} \\[5pt]
\end{eqnarray}となる。接線 l と x 軸との交点 D の x 座標は
\begin{eqnarray}
0 &=& -\frac{1}{a^2}x +\frac{2}{a} \\[5pt]
x &=& 2a \\[5pt]
\end{eqnarray}となる。
これから\[ \mathrm{ OA }^2=\mathrm{ AD }^2=a^2+\frac{1}{a^2} \]がわかるので、余弦定理から
\begin{eqnarray}
\mathrm{ OD }^2 &=& \mathrm{ OA }^2+\mathrm{ AD }^2-2 \mathrm{ OA } \cdot \mathrm{ AD } \cos \angle \mathrm{ OAD } \\[5pt]
4a^2 &=& 2\left(a^2+\frac{1}{a^2}\right)-2\left(a^2+\frac{1}{a^2}\right) \cos \frac{\pi}{6} \\[5pt]
4a^2 &=& (2-\sqrt{3})\left(a^2+\frac{1}{a^2}\right) \\[5pt]
4a^4-(2-\sqrt{3})a^4 &=& 2-\sqrt{3} \\[5pt]
(2+\sqrt{3})a^4 &=& 2-\sqrt{3} \\[5pt]
a^4 &=& \frac{2-\sqrt{3} }{2+\sqrt{3} } \times \frac{2-\sqrt{3} }{2-\sqrt{3} } \\[5pt]
&=& \left(2-\sqrt{3}\right)^2 \\[5pt]
a &=& \sqrt{2-\sqrt{3} }
\end{eqnarray}が得られる。
また、
\begin{eqnarray}
\mathrm{ OA }^2
&=&
a^2 +\frac{1}{a^2} \\[5pt]
&=&
2-\sqrt{3} +\frac{1}{2-\sqrt{3} } \\[5pt]
&=&
2-\sqrt{3} +2+\sqrt{3} \\[5pt]
&=&
4
\end{eqnarray}なので、 $C_2$ の半径は $2$ であることがわかる。
点 $(0,2)$, $(2,0)$ を E, F とする。また、点 A, B から x 軸に下した垂線の足を、それぞれ G, H とする。なお、 $C_1$ と $C_2$ は直線 $y=x$ について対称なので、 $\mathrm{ B } \left(\dfrac{1}{a}, a\right)$ である。
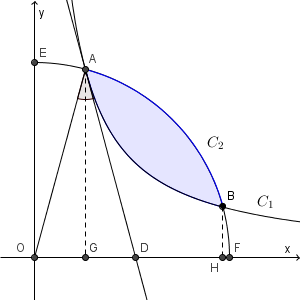
このとき、求める面積は、半径 $2$ の円の面積の $\dfrac{1}{4}$ から
(1) OGAE (AE は $C_2$ 上の曲線)
(2) GHBA (AB は $C_1$ 上の曲線)
(3) HFB (BF は $C_2$ 上の曲線)
で囲まれた部分の面積を引いて求めることができる。
ここで、 $\mathrm{ OG }=\mathrm{ BH }=a$, $\mathrm{ GA }=\mathrm{ HO }=\dfrac{1}{a}$, $\mathrm{ OA }=\mathrm{ BO }=2$ なので、三角形 OAG と三角形 BOH は合同である。よって、上の(1)と(3)の面積の和は、おうぎ形 OAE とおうぎ形 OBF の面積の和となる。また、 $\angle \mathrm{ OAG }=\dfrac{\pi}{12}$ なので、このおうぎ形の中心角は、ともに $\dfrac{\pi}{12}$ となる。
(2)の部分の面積は
\begin{eqnarray}
& &
\int _a^{\frac{1}{a} } \frac{1}{x} dx \\[5pt]
&=&
[\log x]_a^{\frac{1}{a} } \\[5pt]
&=&
\log \frac{1}{a} -\log a \\[5pt]
&=&
-2\log a \\[5pt]
\end{eqnarray}である。
よって、求める面積は
\begin{eqnarray}
& &
2^2 \pi \left(\frac{1}{4} -\frac{1}{24}-\frac{1}{24}\right) +2\log a \\[5pt]
&=&
4 \pi \times \frac{1}{6} +2\log \sqrt{2-\sqrt{3} } \\[5pt]
&=&
\frac{2}{3}\pi +\log (2-\sqrt{3}) \\[5pt]
\end{eqnarray}となる。
(終)
解説
上の解答では、接線の方程式を求めて考えていますが、接線 l の傾きが $-\dfrac{1}{a^2}$ と分かった時点で、三角形 OAD が二等辺三角形になることはわかります。また、 $\angle \mathrm{ OAG }$ もわかるので、 $\tan \dfrac{\pi}{12}=a^2$ から a を求めることもできます。 a や $C_2$ の半径の求め方はいろいろあります。
後半の面積の部分は、上の解答では、円から不要な部分をどんどん取り除く方法で求めました。素直に計算する場合は、次の積分を計算することになります。\[ \int_a^{\frac{1}{a} }\left(\sqrt{4-x^2}-\frac{1}{x}\right)dx \]前半の積分は、置換積分で計算します。 $a$, $\dfrac{1}{a}$ に対応する角は、図形から $\dfrac{5\pi}{12}$, $\dfrac{\pi}{12}$ だから、積分をした値は $\dfrac{2}{3}\pi$ となります。後半の積分も計算すれば、上の解答と同じ結果が得られます。
上の解答では、 $\dfrac{1}{4}$ の円から、不要な部分を引いて求めました。下の図の、 OGAE, GHBA(AB は $C_1$ 上の線), HFB の3つを引きました。このとき、解答中での計算により、 $\dfrac{1}{4}$ の円から、1つ目と3つ目を引いた時点で、中心角が $\dfrac{1}{3}\pi$ のおうぎ形が残ることがわかります。

結果的に、おうぎ形 OAB の面積から GHBA で囲まれた部分の面積を引いた部分が答えになります。2つの領域は重なっていないので、ここだけを見ると、不思議な感じがしますね。しかし、次のように考えてみれば、不思議さはなくなるでしょう。
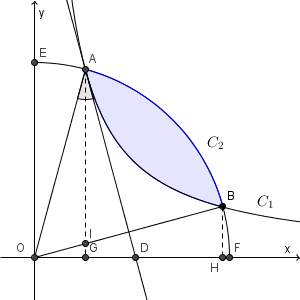
OB と AG の交点を I とすると、三角形 OAG と三角形 BOH が合同であることから、三角形 OAI と四角形 BIGH の面積は等しくなります。よって、おうぎ形OAB の面積は、GHBA(AB は $C_2$ 上の線)の面積と等しくなることがわかります。このことから、おうぎ形の面積から $\displaystyle \int _a^{\frac{1}{a} } \frac{1}{x} dx$ を引けば、答えとなります。





