京都大学文系 2014年度第2問解説

🕒 2017/02/24 🔄 2023/05/01

問題編

問題

　t を実数とする。 $y=x^3-x$ のグラフ C へ点 $\mathrm{ P }(1,t)$ から接線を引く。
(1) 接線がちょうど1本だけ引けるような t の範囲を求めよ。
(2) t が(1)で求めた範囲を動くとき、 $\mathrm{ P }(1,t)$ から C へ引いた接線と C で囲まれた部分の面積を $S(t)$ とする。 $S(t)$ の取りうる値の範囲を求めよ。

考え方

「通る点」を中心に考えるのではなく、「接点」を中心に考えましょう。「接線が1本だけ」というのは、「接点が1点だけ」と言い換えて考えていきます。この考え方を使った問題は入試ではよく出題されるので、見たことがある人は多いでしょう。

(2)も、接点を中心に考えていきます。接点以外の共有点の座標は、簡単に求められます。接点がどの範囲を動くかに注意して、面積の範囲を求めましょう。

解答編

問題

　t を実数とする。 $y=x^3-x$ のグラフ C へ点 $\mathrm{ P }(1,t)$ から接線を引く。
(1) 接線がちょうど1本だけ引けるような t の範囲を求めよ。
(2) t が(1)で求めた範囲を動くとき、 $\mathrm{ P }(1,t)$ から C へ引いた接線と C で囲まれた部分の面積を $S(t)$ とする。 $S(t)$ の取りうる値の範囲を求めよ。

解答

(1)
$f(x)=x^3-x$ とする。また、接点の x 座標を s とおく。

$f'(x)=3x^2-1$ なので、 $(s,f(s))$ における接線の方程式は
\begin{eqnarray} y -(s^3-s) &=& (3s^2-1)(x-s) \\ y &=& (3s^2-1)x -3s^3+s +s^3-s \\ &=& (3s^2-1)x -2s^3 \\ \end{eqnarray}となる。これが $\mathrm{ P }(1,t)$ を通るとすると \begin{eqnarray} t &=& (3s^2-1)\cdot 1 -2s^3 \\ &=& -2s^3 +3s^2 -1 \\ \end{eqnarray}が成り立つ。この右辺を $g(s)$ とおく。 s は接点の x 座標なので、接線がちょうど1本だけ引けることは、 $t=g(s)$ を満たす s が1つしかないことと同値である。

ここで
\begin{eqnarray} g'(s) &=& -6s^2 +6s \\ &=& -6s(s-1) \\ \end{eqnarray}なので、増減表は次のようになる。 \begin{array}{c|ccccc} s & \cdots & 0 & \cdots & 1 & \cdots \\ \hline g' & - & 0 & + & 0 & - \\ \hline g & \searrow & -1 & \nearrow & 0 & \searrow \end{array}となる。また、 \begin{eqnarray} -2s^3 +3s^2 -1 &=& (s-1)(-2s^2+s+1) \\ &=& (s-1)^2(-2s-1) \\ \end{eqnarray}なので、 $y=g(s)$ のグラフは次のようになる。

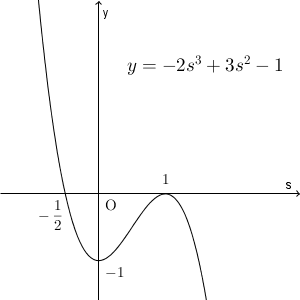
よって、 $t=g(s)$ を満たす s が1つだけとなるような t の範囲は、\[ t\lt -1, \ t\gt 0 \]となる。

(2)
(1)のグラフより、 $t\gt 0$ と $s\lt -\dfrac{1}{2}$ は同値である。また、グラフと
\begin{eqnarray} -2s^3 +3s^2 -1 &=& -1 \\ s^2(2s-3) &=& 0 \\ \end{eqnarray}から、 $t\lt -1$ と $s \gt \dfrac{3}{2}$ は同値であることがわかる。

以下では、 $S(t)$ を s を用いて表し、 $\displaystyle s\lt -\dfrac{1}{2}, \ s \gt \dfrac{3}{2}$ の範囲を動くときに取りうる値を求める。

接線と C との共有点の x 座標は
\begin{eqnarray} x^3-x &=& (3s^2-1)x -2s^3 \\ x^3 -3s^2x +2s^3 &=& 0 \\ (x-s)(x^2+sx-2s^2) &=& 0 \\ (x-s)^2(x+2s) &=& 0 \\ \end{eqnarray}から、 $s,-2s$ であることがわかる。

よって、
\begin{eqnarray} S(t) &=& \left| \int_{-2s}^s (x^3 -3s^2x +2s^3) dx \right| \\[5pt] &=& \left| \left[ \frac{x^4}{4} -\frac{3s^2x^2}{2} +2s^3x \right]_{-2s}^s \right| \\[5pt] &=& \left| \left( \frac{s^4}{4} -\frac{3s^4}{2} +2s^4 \right) -\left( 4s^4 -6s^4 -4s^4 \right) \right| \\[5pt] &=& \left| \frac{-5s^4}{4} +2s^4 +6s^4 \right| \\[5pt] &=& \frac{27s^4}{4} \\[5pt] \end{eqnarray}となる。ここで、 s は $\displaystyle s\lt -\dfrac{1}{2}, \ s \gt \dfrac{3}{2}$ の範囲を動くので、 \begin{eqnarray} S(t) &=&\frac{27s^4}{4} \\[5pt] &\gt& \frac{27}{4} \times \left(-\frac{1}{2}\right)^4 \\[5pt] &=& \frac{27}{64} \end{eqnarray}となる。 $S(t)$ はこの範囲の値をすべて取るので、求める範囲は\[ S(t) \gt \frac{27}{64} \]となる。

（終）