センター試験 数学II・数学B 2014年度 第4問 解説
【選択問題】(第3問~第6問から2問選択)
問題編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$座標空間において、立方体 OABC-DEFG の頂点を
$\mathrm{ O }(0,0,0)$, $\mathrm{ A }(3,0,0)$, $\mathrm{ B }(3,3,0)$, $\mathrm{ C }(0,3,0)$, $\mathrm{ D }(0,0,3)$, $\mathrm{ E }(3,0,3)$, $\mathrm{ F }(3,3,3)$, $\mathrm{ G }(0,3,3)$
とし、 OD を $2:1$ に内分する点を K, OA を $1:2$ に内分する点を L とする。 BF 上の点 M, FG 上の点 N および K, L の4点は同一平面上にあり、四角形 KLMN は平行四辺形であるとする。(1) 四角形 KLMN の面積を求めよう。ベクトル $\overrightarrow{ \mathrm{ LK } }$ を成分で表すと\[ \overrightarrow{ \mathrm{ LK } }=\left( \myBox{アイ}, \myBox{ウ}, \myBox{エ} \right) \]となり、四角形 KLMN が平行四辺形であることにより、 $\overrightarrow{ \mathrm{ LK } } = \myBox{オ}$ である。 $\myBox{オ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
0: $\overrightarrow{ \mathrm{ ML } }$, 1: $\overrightarrow{ \mathrm{ LM } }$, 2: $\overrightarrow{ \mathrm{ NM } }$, 3: $\overrightarrow{ \mathrm{ MN } }$
ここで、 $\mathrm{ M }(3,3,s)$, $\mathrm{ N }(t,3,3)$ と表すと、 $\overrightarrow{ \mathrm{ LK } }=\mybox{オ}$ であるので、 $s=\myBox{カ}$, $t=\myBox{キ}$ となり、 N は FG を $1:\myBox{ク}$ に内分することがわかる。
また、 $\overrightarrow{ \mathrm{ LK } }$ と $\overrightarrow{ \mathrm{ LM } }$ について\[ \overrightarrow{ \mathrm{ LK } } \cdot \overrightarrow{ \mathrm{ LM } } = \myBox{ケ},\ \left| \overrightarrow{ \mathrm{ LK } } \right| = \sqrt{\myBox{コ} },\ \left| \overrightarrow{ \mathrm{ LM } } \right| = \sqrt{\myBox{サシ} } \]となるので、四角形 KLMN の面積は $\sqrt{\myBox{スセ} }$ である。(2) 四角形 KLMN を含む平面を $\alpha$ とし、点 O を通り平面 $\alpha$ と垂直に交わる直線を l, $\alpha$ と l の交点を P とする。 $\left| \overrightarrow{ \mathrm{ OP } } \right|$ と三角錐 OLMN の体積を求めよう。
$\mathrm{ P }(p,q,r)$ とおくと、 $\overrightarrow{ \mathrm{ OP } }$ は $\overrightarrow{ \mathrm{ LK } }$ および $\overrightarrow{ \mathrm{ LM } }$ と垂直であるから、\[ \overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LK } } = \overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LM } } = \myBox{ソ} \]となるので、 $p=\myBox{タ}r$, $\displaystyle q=\frac{\myBox{チツ} }{\myBox{テ} }r$ であることがわかる。 $\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ PL } }$ が垂直であることにより $\displaystyle r=\frac{\myBox{ト} }{\myBox{ナニ} }$ となり、 $\left| \overrightarrow{ \mathrm{ OP } } \right|$ を求めると\[ \left| \overrightarrow{ \mathrm{ OP } } \right| = \frac{\myBox{ヌ} \sqrt{ \myBox{ネノ} } }{ \myBox{ハヒ} } \]である。 $\left| \overrightarrow{ \mathrm{ OP } } \right|$ は三角形 LMN を底面とする三角錐 OLMN の高さであるから、三角錐 OLMN の体積は $\myBox{フ}$ である。
考え方
空間ベクトルなので、拒否反応が出る人もいるかもしれません。しかし、出てくる図形はきれいだし、計算量は少なめなので、図を描いて考えればそれほど難しくはないでしょう。
(1)は頭の中で考えずに、図を描けば間違いは減るはずです。日頃から、図を正しく描く練習をしましょう。
(2)は垂直を「内積0」に置き換え、成分で考えて解いていきます。最後の体積を求める際、底面積を求めなければいけませんが、(1)の結果を使えばすぐに出せます。
【選択問題】(第3問~第6問から2問選択)
解答編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$座標空間において、立方体 OABC-DEFG の頂点を
$\mathrm{ O }(0,0,0)$, $\mathrm{ A }(3,0,0)$, $\mathrm{ B }(3,3,0)$, $\mathrm{ C }(0,3,0)$, $\mathrm{ D }(0,0,3)$, $\mathrm{ E }(3,0,3)$, $\mathrm{ F }(3,3,3)$, $\mathrm{ G }(0,3,3)$
とし、 OD を $2:1$ に内分する点を K, OA を $1:2$ に内分する点を L とする。 BF 上の点 M, FG 上の点 N および K, L の4点は同一平面上にあり、四角形 KLMN は平行四辺形であるとする。(1) 四角形 KLMN の面積を求めよう。ベクトル $\overrightarrow{ \mathrm{ LK } }$ を成分で表すと\[ \overrightarrow{ \mathrm{ LK } }=\left( \myBox{アイ}, \myBox{ウ}, \myBox{エ} \right) \]となり、四角形 KLMN が平行四辺形であることにより、 $\overrightarrow{ \mathrm{ LK } } = \myBox{オ}$ である。 $\myBox{オ}$ に当てはまるものを、次の 0 ~ 3 のうちから一つ選べ。
0: $\overrightarrow{ \mathrm{ ML } }$, 1: $\overrightarrow{ \mathrm{ LM } }$, 2: $\overrightarrow{ \mathrm{ NM } }$, 3: $\overrightarrow{ \mathrm{ MN } }$
解説
図は次のようになっています。
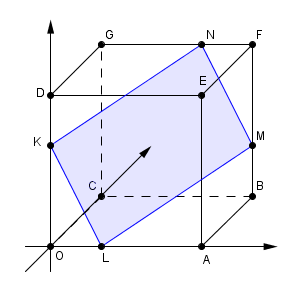
$\overrightarrow{ \mathrm{ OK } }=(0,0,2)$, $\overrightarrow{ \mathrm{ OL } }=(1,0,0)$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ LK } }
&=&
\overrightarrow{ \mathrm{ OK } } -\overrightarrow{ \mathrm{ OL } } \\
&=&
(0,0,2)-(1,0,0) \\
&=&
(-1,0,2) \\
\end{eqnarray}となります。
また、四角形 KLMN は平行四辺形なので、 $\overrightarrow{ \mathrm{ LK } } = \overrightarrow{ \mathrm{ MN } }$ となることがわかります。
解答
アイウエ:-102
オ:3
解答編 つづき
問題
ここで、 $\mathrm{ M }(3,3,s)$, $\mathrm{ N }(t,3,3)$ と表すと、 $\overrightarrow{ \mathrm{ LK } }=\mybox{オ}$ であるので、 $s=\myBox{カ}$, $t=\myBox{キ}$ となり、 N は FG を $1:\myBox{ク}$ に内分することがわかる。
解説

$\overrightarrow{ \mathrm{ MN } }$ を成分を使って表すと
\begin{eqnarray}
\overrightarrow{ \mathrm{ MN } }
&=&
\overrightarrow{ \mathrm{ ON } } -\overrightarrow{ \mathrm{ OM } } \\
&=&
(t,3,3) -(3,3,s) \\
&=&
(t-3,0,3-s) \\
\end{eqnarray}となります。これが $\overrightarrow{ \mathrm{ LK } }=(-1,0,2)$ と等しいので、成分を比較して $3-s=2$ から $s=1$, $t-3=-1$ から $t=2$ が得られます。
$\mathrm{ N }(2,3,3)$ なので、これは FG を $1:2$ に内分する点であることがわかります。
解答
カキ:12
ク:2
解答編 つづき
問題
また、 $\overrightarrow{ \mathrm{ LK } }$ と $\overrightarrow{ \mathrm{ LM } }$ について\[ \overrightarrow{ \mathrm{ LK } } \cdot \overrightarrow{ \mathrm{ LM } } = \myBox{ケ},\ \left| \overrightarrow{ \mathrm{ LK } } \right| = \sqrt{\myBox{コ} },\ \left| \overrightarrow{ \mathrm{ LM } } \right| = \sqrt{\myBox{サシ} } \]となるので、四角形 KLMN の面積は $\sqrt{\myBox{スセ} }$ である。
解説

$\overrightarrow{ \mathrm{ LK } }=(-1,0,2)$ であり、
\begin{eqnarray}
\overrightarrow{ \mathrm{ LM } }
&=&
(3,3,1)-(1,0,0) \\
&=&
(2,3,1) \\
\end{eqnarray}なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ LK } } \cdot \overrightarrow{ \mathrm{ LM } }
&=&
(-1,0,2) \cdot (2,3,1) \\
&=&
-2+0+2=0
\end{eqnarray}となります。つまり、 LK と LM は垂直に交わるということです。四角形 KLMN は、実は長方形だったんですね。
また、
\begin{eqnarray}
\left| \overrightarrow{ \mathrm{ LK } } \right|
&=&
\sqrt{ (-1)^2+0^2+2^2 } \\
&=&
\sqrt{ 1+4 } = \sqrt{5} \\
\end{eqnarray}であり、
\begin{eqnarray}
\left| \overrightarrow{ \mathrm{ LM } } \right|
&=&
\sqrt{ 2^2+3^2+1^2 } \\
&=&
\sqrt{ 4+9+1 } = \sqrt{14} \\
\end{eqnarray}であるので、四角形 KLMN の面積は
\begin{eqnarray}
\sqrt{5} \times \sqrt{14} = \sqrt{70}
\end{eqnarray}であることがわかります。
解答
ケコサシ:0514スセ:70
解答編 つづき
問題
(2) 四角形 KLMN を含む平面を $\alpha$ とし、点 O を通り平面 $\alpha$ と垂直に交わる直線を l, $\alpha$ と l の交点を P とする。 $\left| \overrightarrow{ \mathrm{ OP } } \right|$ と三角錐 OLMN の体積を求めよう。
$\mathrm{ P }(p,q,r)$ とおくと、 $\overrightarrow{ \mathrm{ OP } }$ は $\overrightarrow{ \mathrm{ LK } }$ および $\overrightarrow{ \mathrm{ LM } }$ と垂直であるから、\[ \overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LK } } = \overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LM } } = \myBox{ソ} \]となるので、 $p=\myBox{タ}r$, $\displaystyle q=\frac{\myBox{チツ} }{\myBox{テ} }r$ であることがわかる。
解説
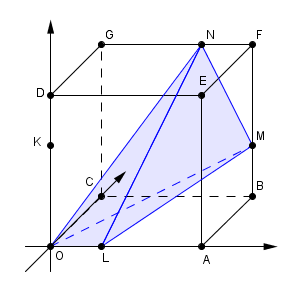
OP は平面 $\alpha$ と垂直に交わるので、この平面上にあるベクトルとは垂直になります。よって、 $\overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LK } }$ も $\overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LM } }$ も垂直なベクトルの内積なので、ともに $0$ となります。
成分を使って表すと
\begin{eqnarray}
\overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LK } }
&=&
(p,q,r) \cdot (-1,0,2) \\
&=&
-p+2r \\
\end{eqnarray}が $0$ になることから、 $p=2r$ が得られます。
また、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ LM } }
&=&
(p,q,r) \cdot (2,3,1) \\
&=&
2p+3q+r \\
\end{eqnarray}も $0$ になります。 $p=2r$ を使うと
\begin{eqnarray}
2p+3q+r &=& 0 \\
4r+3q+r &=& 0 \\
q &=& \frac{-5}{3}r \\
\end{eqnarray}が得られます。
解答
ソ:0
タチツテ:2-53
解答編 つづき
問題
$\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ PL } }$ が垂直であることにより $\displaystyle r=\frac{\myBox{ト} }{\myBox{ナニ} }$ となり、 $\left| \overrightarrow{ \mathrm{ OP } } \right|$ を求めると\[ \left| \overrightarrow{ \mathrm{ OP } } \right| = \frac{\myBox{ヌ} \sqrt{ \myBox{ネノ} } }{ \myBox{ハヒ} } \]である。
解説
$\overrightarrow{ \mathrm{ OP } }$ と $\overrightarrow{ \mathrm{ PL } }$ も垂直なので、この内積は $0$ になります。この内積を成分を使って書くと
\begin{eqnarray}
\overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ PL } }
&=&
(p,q,r) \cdot (1-p,-q,-r) \\
&=&
p(1-p)-q^2-r^2
\end{eqnarray}となります。これが $0$ になることと、 $p=2r$, $\displaystyle q=-\frac{5}{3}r$ が成り立つことから
\begin{eqnarray}
2r(1-2r)-\left(-\frac{5}{3}r \right)^2 -r^2 &=& 0 \\[5pt]
2r-4r^2-\frac{25}{9}r^2 -r^2 &=& 0 \\[5pt]
2r-\frac{70}{9}r^2 &=& 0 \\[5pt]
r\left(1-\frac{35}{9}r\right) &=& 0 \\[5pt]
\end{eqnarray}となります。 $r=0$ とすると、 P は原点になってしまうので、 $r\ne 0$ となります。このことから、 $\displaystyle 1-\frac{35}{9}r=0$ 、つまり、\[ r=\frac{9}{35} \]が得られます。
また、
\begin{eqnarray}
\left| \overrightarrow{ \mathrm{ OP } } \right|
&=&
\sqrt{p^2+q^2+r^2} \\[5pt]
&=&
\sqrt{(2r)^2+\left(-\frac{5}{3}r\right)^2+r^2} \\[5pt]
&=&
\sqrt{4r^2+\frac{25}{9}r^2+r^2} \\[5pt]
&=&
\sqrt{\frac{70}{9} }r \\[5pt]
&=&
\frac{\sqrt{70} }{3} \times \frac{9}{35} \\[5pt]
&=&
\frac{3\sqrt{70} }{35} \\[5pt]
\end{eqnarray}が得られます。
解答
トナニ:935
ヌネノハヒ:37035
解答編 つづき
問題
$\left| \overrightarrow{ \mathrm{ OP } } \right|$ は三角形 LMN を底面とする三角錐 OLMN の高さであるから、三角錐 OLMN の体積は $\myBox{フ}$ である。
解説

三角錐 OLMN について、三角形 LMN を底面と考えると、高さは OP になります。底面の三角形 LMN は(1)で求めた四角形 KLMN の半分なので、面積は $\displaystyle \frac{\sqrt{70} }{2}$ となります。また、高さはさきほど求めた通り $\displaystyle \frac{3\sqrt{70} }{35}$ です。よって、この三角錐の体積は
\begin{eqnarray} \frac{1}{3} \times \frac{\sqrt{70} }{2} \times \frac{3\sqrt{70} }{35} &=& 1 \end{eqnarray}と求めることができます。
解答
フ:1





