センター試験 数学II・数学B 2014年度 第1問 [1] 解説
【必答問題】
問題編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$O を原点とする座標平面において、点 $\mathrm{ P }(p,q)$ を中心とする円 C が、方程式 $\displaystyle y=\frac{4}{3}x$ で表される直線 l に接しているとする。
(1) 円 C の半径 r を求めよう。
点 P を通り直線 l に垂直な直線の方程式は\[ y=-\frac{\myBox{ア} }{\myBox{イ} }(x-p)+q \]なので、 P から l に引いた垂線と l との交点 Q の座標は\[ \left( \frac{3}{25} \left(\ \myBox{ウ}p+\myBox{エ}q \ \right), \ \frac{4}{25} \left(\ \mybox{ウ}p+\mybox{エ}q \ \right) \right) \]となる。
求める C の半径 r は、 P と l の距離 PQ に等しいので\[ r=\frac{1}{5} \left| \ \myBox{オ}p-\myBox{カ}q \ \right| \ \cdots ① \]である。(2) 円 C が、 x 軸に接し、点 $\mathrm{ R }(2,2)$ を通る場合を考える。このとき、 $p\gt 0$, $q\gt 0$ である。 C の方程式を求めよう。
C は x 軸に接するので、 C の半径 r は q に等しい、したがって、①により、 $p=\myBox{キ}q$ である。
C は点 R を通るので、求める C の方程式は\[ \left( x-\myBox{ク} \right)^2+\left( y-\myBox{ケ} \right)^2=\myBox{コ} \ \cdots ② \]または\[ \left( x-\myBox{サ} \right)^2+\left( y-\myBox{シ} \right)^2=\myBox{ス} \ \cdots ③ \]であることがわかる。ただし、 $\mybox{コ}\lt\mybox{ス}$ とする。(3) 方程式②の表す円の中心を S 、方程式③の表す円の中心を Tとおくと、直線 ST は原点 O を通り、点 O は線分 ST を $\myBox{セ}$ する。 $\myBox{セ}$ に当てはまるものを、次の0~5のうちから一つ選べ。
0: $1:1$ に内分
1: $1:2$ に内分
2: $2:1$ に内分
3: $1:1$ に外分
4: $1:2$ に外分
5: $2:1$ に外分
考え方
わかりにくい誘導も少なく、計算が難しい個所も少ないため、解きやすいと思います。円と直線が接するときに、円と直線の距離が円の半径と一致する、という考え方はいろんな場面でよく使います。
【必答問題】
解答編
問題
$\def\myBox#1{\bbox[3px, border:2px solid]{\ \bf{ #1 }\ } }\def\mybox#1{\bbox[4px, border:1px solid gray]{\ #1\ } }$O を原点とする座標平面において、点 $\mathrm{ P }(p,q)$ を中心とする円 C が、方程式 $\displaystyle y=\frac{4}{3}x$ で表される直線 l に接しているとする。
(1) 円 C の半径 r を求めよう。
点 P を通り直線 l に垂直な直線の方程式は\[ y=-\frac{\myBox{ア} }{\myBox{イ} }(x-p)+q \]なので、 P から l に引いた垂線と l との交点 Q の座標は\[ \left( \frac{3}{25} \left(\ \myBox{ウ}p+\myBox{エ}q \ \right), \ \frac{4}{25} \left(\ \mybox{ウ}p+\mybox{エ}q \ \right) \right) \]となる。
解説
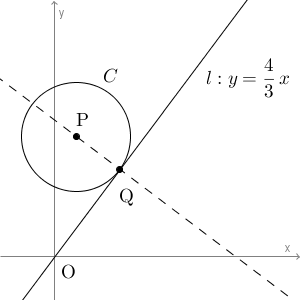
直線 l に垂直な直線の傾きは、直線 l の傾きとの積が $-1$ になるので、 $\displaystyle -\frac{3}{4}$ となります。よって、直線 l に垂直な直線の方程式は\[ y=-\frac{3}{4}(x-p)+q \]となります。
Q は2直線の交点なので、連立方程式を解けば求められますね。
\begin{eqnarray}
\frac{4}{3}x &=& -\frac{3}{4}(x-p)+q \\[5pt]
16x &=& -9(x-p)+12q \\[5pt]
25x &=& 9p+12q \\[5pt]
x &=& \frac{3}{25}(3p+4q) \\
\end{eqnarray}となります。これを l の方程式に入れれば
\begin{eqnarray}
y &=& \frac{4}{3} \times \frac{3}{25}(3p+4q) \\[5pt]
&=& \frac{4}{25}(3p+4q) \\[5pt]
\end{eqnarray}となります。
解答
アイ:34ウエ:34
解答編 つづき
問題
求める C の半径 r は、 P と l の距離 PQ に等しいので\[ r=\frac{1}{5} \left| \ \myBox{オ}p-\myBox{カ}q \ \right| \ \cdots ① \]である。
解説
$\mathrm{ P }(p,q)$ と $l: 4x-3y=0$ との距離は、点と直線の距離の公式から\begin{eqnarray} \frac{|4p-3q|}{\sqrt{4^2+(-3)^2} } &=& \frac{|4p-3q|}{5} \end{eqnarray}となります。これが半径 r と一致します。
解答
オカ:43解答編 つづき
問題
(2) 円 C が、 x 軸に接し、点 $\mathrm{ R }(2,2)$ を通る場合を考える。このとき、 $p\gt 0$, $q\gt 0$ である。 C の方程式を求めよう。
C は x 軸に接するので、 C の半径 r は q に等しい、したがって、①により、 $p=\myBox{キ}q$ である。
解説
円 C が、 x 軸に接し、点 $\mathrm{ R }(2,2)$ を通る場合、円の中心は、直線 l と x 軸の間の領域にないといけないため、 $p,q\gt 0$ となります。
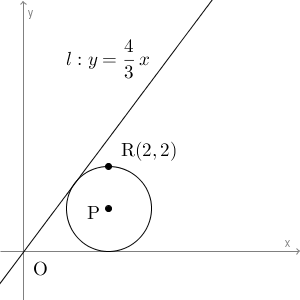
C が x 軸に接するとき、中心の y 座標である q は半径 r と一致します。なので、①より
\begin{eqnarray}
q &=& \frac{|4p-3q|}{5} \\
5q &=& |4p-3q| \\
\end{eqnarray}両辺は正なので二乗して
\begin{eqnarray}
16p^2-24pq+9q^2 &=& 25q^2 \\
16p^2-24pq -16q^2 &=& 0 \\
2p^2-3pq -2q^2 &=& 0 \\
(2p+q)(p-2q) &=& 0 \\
p &=& 2q, -\frac{q}{2}
\end{eqnarray}$p,q$ が正なので、 $p=2q$ となります。
解答
キ:2解答編 つづき
問題
C は点 R を通るので、求める C の方程式は\[ \left( x-\myBox{ク} \right)^2+\left( y-\myBox{ケ} \right)^2=\myBox{コ} \ \cdots ② \]または\[ \left( x-\myBox{サ} \right)^2+\left( y-\myBox{シ} \right)^2=\myBox{ス} \ \cdots ③ \]であることがわかる。ただし、 $\mybox{コ}\lt\mybox{ス}$ とする。
解説
先ほどの答えから、 $p=2q$ とかけます。また、半径は q だったので、円 C の方程式は次のように書けます。\[ (x-2q)^2+(y-q)^2=q^2 \]これが点 $\mathrm{ R }(2,2)$ と通るので\begin{eqnarray} (2-2q)^2+(2-q)^2 &=& q^2 \\ 4q^2-8q+4 +q^2-4q+4 &=& q^2 \\ 4q^2-12q+8 &=& 0 \\ q^2-3q+2 &=& 0 \\ (q-1)(q-2) &=& 0 \\ \end{eqnarray}となります。
$q=1$ のとき、円 C の方程式は\[ (x-2)^2+(y-1)^2=1 \]となり、 $q=2$ のときは\[ (x-4)^2+(y-2)^2=4 \]となります。
解答
クケコ:211サシス:424
解答編 つづき
問題
(3) 方程式②の表す円の中心を S 、方程式③の表す円の中心を Tとおくと、直線 ST は原点 O を通り、点 O は線分 ST を $\myBox{セ}$ する。 $\myBox{セ}$ に当てはまるものを、次の0~5のうちから一つ選べ。
0: $1:1$ に内分
1: $1:2$ に内分
2: $2:1$ に内分
3: $1:1$ に外分
4: $1:2$ に外分
5: $2:1$ に外分
解説
先ほど求めた円の方程式から、 S,T の座標は、それぞれ $(2,1)$, $(4,2)$ となることがわかります。\[ 0 = \frac{-2\cdot 2+1\cdot 4}{1-2} = \frac{-2\cdot 1+1\cdot 2}{1-2} \]となるので、 O は線分 ST を $1:2$ に外分する点であることがわかります。





