【標準】無理関数のグラフと不等式

🕒 2018/06/25 🔄 2023/06/22

ここでは、無理関数を含んだ不等式を見ていきます。グラフを用いる方法で解いていきます。

📘 目次

無理関数と不等式

例題

次の不等式を解きなさい。\[ \sqrt{x+5}\gt x-1 \]

左辺にルートがあるので、2乗してルートを消したくなりますね。しかし、単純に両辺を2乗してはいけません。両辺が0以上の場合は2乗してもいいですが、負の場合は不等号の向きが変わってしまいます。 $1\gt -2$ ですが、両辺を2乗すると $1\lt 4$ となり、不等号の向きが変わってますね。

両辺を2乗する方法は後で見てみることにして、まずは無理関数のグラフを利用して解く方法を考えましょう。

$y=\sqrt{x+5}$ は、 $y=\sqrt{x}$ を $x$ 軸方向に $-5$ だけ平行移動したものです。グラフは次のようになります。

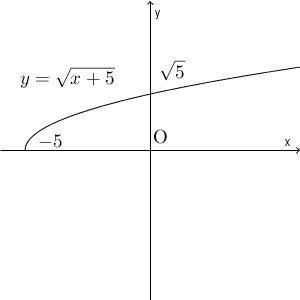
ここに、 $y=x-1$ のグラフを追加しましょう。

グラフを見ると、交点の座標を求める必要があることがわかりますね。
\begin{eqnarray} \sqrt{x+5} &=& x-1 \\[5pt] x+5 &=& (x-1)^2 \\[5pt] x^2-3x-4 &=& 0 \\[5pt] (x-4)(x+1) &=& 0 \\[5pt] x &=& -1,4 \\[5pt] \end{eqnarray}となります。ここで、 $y=\sqrt{x+5}$ の値域は0以上なので、交点は、 $(4,3)$ となることがわかります。もう一つの解に対応する点 $(-1,-2)$ は、交点ではないことに注意しましょう。

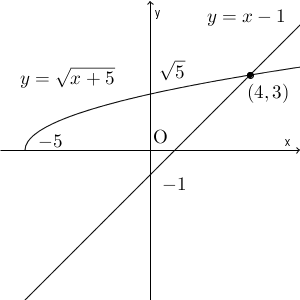
グラフを見て、無理関数の方が上になっている部分を答えればいいですね。これより、\[ -5\leqq x \lt 4 \]が解となることがわかります。

ちなみに、先ほど $(-1,-2)$ が交点ではない、と書きましたが、ではこれは何なのでしょうか。なぜ交点ではないのに出てきたのでしょう。

この交点の正体を見るには、 $y=-\sqrt{x+5}$ のグラフを追加するとわかります。

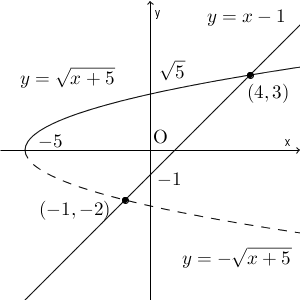
$\sqrt{x+5}=x-1$ を解くときに、両辺を2乗しましたね。そのときに得られる式は、 $-\sqrt{x+5}=x-1$ の両辺を2乗したときの式と同じになります。この2つが混じって出てきたわけですね。

しかし、無理関数の値域は限定されているため、得られた交点がすべて対象であるとは限りません。得られた交点が元の無理関数のグラフ上にあるかどうかを確認する必要があります。

今まで、一次方程式や二次方程式を解いたときに、「解がちゃんと条件式を満たしているか」を確認することはありませんでした。しかし、ここでは確認する必要がありました。この違いは、同値な式変形を行っているかどうか、によって生まれています。

一般的に、「 $a=b$ ならば $a^2=b^2$ 」は成り立ちますが、「 $a^2=b^2$ ならば $a=b$ 」とは限りません。上で行った変形では、両辺を2乗したため、同値な式変形ではないんですね。得られた答えは、「条件を満たしているとすれば、これだ」と言っているだけで、「これらが条件を満たしている」までは言えません。

両辺を2乗すると、同値な式変形にならない、という点に注意しましょう。

別の解き方

先ほどの例題を、別の解き方で考えてみます。両辺を2乗する方法で考えてみましょう。

\[ \sqrt{x+5}\gt x-1 \]の左辺・右辺の符号で場合分けをして考えます。符号によって、2乗したときの結果が変わってくるからですね。

といっても、左辺は0以上であることが確定しています。なので、右辺がどうなっているかを考えるだけでかまいません。

まず、左辺の定義域より、 $x\geqq -5$ であることをおさえておきます。右辺が負の場合、つまり、 $x\lt 1$ の場合、左辺は0以上なので、不等式はつねに成り立ちます。よって、 $-5\leqq x \lt 1$ の場合、不等式が成り立つことがわかります。

次に、右辺が0以上の場合、つまり、 $x\geqq 1$ の場合を考えましょう。両辺が0以上なので、両辺を2乗することができます。\[ a,b\geqq 0 \ +\textsf{のとき、} a\gt b \iff a^2\gt b^2 \]が成り立つからです。これより、
\begin{eqnarray} x+5 & \gt & (x-1)^2 \\[5pt] -x^2+3x+4 & \gt & 0 \\[5pt] x^2-3x-4 & \lt & 0 \\[5pt] (x+1)(x-4) & \lt & 0 \\[5pt] \end{eqnarray}なので、 $-1\lt x \lt 4$ となることがわかります。もともと $x\geqq 1$ の場合を考えていたので、 $1\leqq x \lt 4$ となります。

2つの場合を合わせると、 $-5\leqq x \lt 4$ となることがわかります。