【標準】連立不等式と領域
ここでは、2つの式の積が正になる領域、負になる領域を求める問題を見ていきます。見た目は連立不等式ではありませんが、問題を解いている途中で出てきます。
2つの積が正になる領域
$(x+y)$ と $(2x-y+4)$ という2つの式の積が正となる領域ですね。「掛けて正」ということは、「両方正」か「両方負」のどちらかしかありません。このどちらかであればいいので、それぞれの領域をくっつけたものが、求める領域となります。
では、まず、両方正の場合を考えてみましょう。
\begin{eqnarray}
\left\{
\begin{array}{l}
x+y \gt 0 \\
2x-y+4 \gt 0
\end{array}
\right.
\end{eqnarray}の場合ですね。これを変形すると、
\begin{eqnarray}
\left\{
\begin{array}{l}
y \gt -x \\
y \lt 2x+4
\end{array}
\right.
\end{eqnarray}となります。【基本】連立不等式と領域のときと同じように考えると、この連立不等式が表す領域は、次のようになります。この場合は、2つの領域を同時に満たす部分(重なっている部分)が対象です。

なお、不等号に等号が含まれていないので、境界線上の点は含みません。
次に、両方が負になる場合を考えましょう。
\begin{eqnarray}
\left\{
\begin{array}{l}
x+y \lt 0 \\
2x-y+4 \lt 0
\end{array}
\right.
\end{eqnarray}の場合ですね。これも同様に変形して
\begin{eqnarray}
\left\{
\begin{array}{l}
y \lt -x \\
y \gt 2x+4
\end{array}
\right.
\end{eqnarray}となります。このように変形してもいいのですが、「両方正」の場合と比べると、不等号の向きが変わっているだけなので、先ほど考えていた領域の上下を反転させるだけでも大丈夫です(実際、変形後の表す領域と一致しています)。
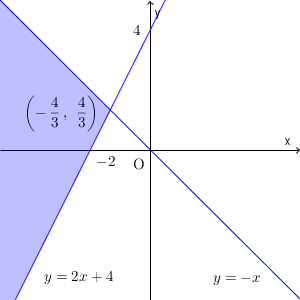
先ほど $y=-x$ より上だと考えていた部分を下にして、 $y=2x+4$ より下だと考えていた部分を上にすれば、「両方負」の場合になります。ここでも、境界線上の点は含みません。
以上から、この2つの領域を合わせた部分が、求める領域となります。
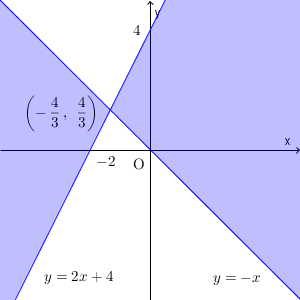
求める領域は、「上の図の色のついた部分。ただし、境界線上の点は除く」となります。
このように、領域が、2つ以上の部分に分割されることもあります。
関連する他の例
係数が同じで、不等号が変わった場合にどうなるかを考えてみましょう。
まず、等号が入った場合を考えましょう。\[ (x+y)(2x-y+4) \geqq 0 \]これもさきほどと同じように、「両方が0以上」「両方が0以下」と分けて考えることができます。両方の領域をくっつけて、次のように求められます。
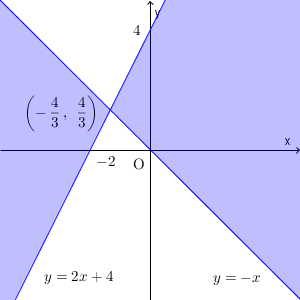
上の図の色のついた部分(境界線上の点を含む)となります。先ほどの例題を元に考えれば、「 $(x+y)(2x-y+4)$ が $0$ か正となる部分」なので、例題の答えに、 $(x+y)(2x-y+4)=0$ となる部分、つまり、境界線上の点を含めたものが、求める領域になります。
次に、不等号の向きが反対になった場合を考えましょう。\[ (x+y)(2x-y+4) \lt 0 \]これも、「1つ目が正、2つ目が負」と「1つ目が負、2つ目が正」と分けて考えていきます。
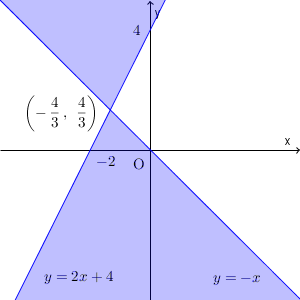
上の図の色のついた部分(境界線上の点は除く)となります。なお、「 $(x+y)(2x-y+4)$ が0以上、ではない部分」と考えれば、先ほど求めた部分「じゃない部分」と一致することも理解できるでしょう。
基本的に、積が正とか負になる領域は、それぞれの式の正負について考え、答えをくっつける、という解き方になります。
おわりに
ここでは、式の積が正とか負になる領域について見てきました。それぞれの式の正負で場合分けをし、それぞれのケースで連立不等式を解いて、最後に答えをくっつける、という方法で解いていきます。場合分けがあって大変に見えますが、境界線は同じなので、それほど大変ではないでしょう。





