【標準】座標を使った中線定理の証明
ここでは、中線定理を、座標を使って証明します。座標で考えることで、計算だけで証明を進めることができます。計算量を減らすコツとともに見ていきましょう。
中線定理
中線定理(parallelogram law)とは、次のような内容です。
頂点と、その対辺の中点を結んだ線を中線と言います。上の定理でいえば、 AM が中線ということです。中線が出てくる定理なので、中線定理というんですね。
これを証明する方法はいろいろありますが、以下では、座標を使った証明方法を見ていきます。
座標を使った中線定理の証明
座標を使えば、ただ単に計算するだけです。
とりあえず、3つの頂点を文字で置きましょう。 $\mathrm{ A }(a_1,a_2)$, $\mathrm{ B }(b_1,b_2)$, $\mathrm{ C }(c_1,c_2)$ とします。また、 BC の中点 M の座標は、【標準】中点の座標で見たように\[ \left(\frac{b_1+c_1}{2}, \frac{b_2+c_2}{2}\right) \]となります。
以上から、左辺
\begin{eqnarray}
& &
\mathrm{AB}^2 +\mathrm{AC}^2 \\[5pt]
&=&
(b_1-a_1)^2+(b_2-a_2)^2 +(c_1-a_1)^2+(c_2-a_2)^2 \\[5pt]
\end{eqnarray}と右辺
\begin{eqnarray}
& &
2(\mathrm{ AM }^2 +\mathrm{ BM }^2) \\[5pt]
&=&
2 \left\{\left(\frac{b_1+c_1}{2}-a_1\right)^2 +\left(\frac{b_2+c_2}{2}-a_2\right)^2 \right\} \\
& &
+2 \left\{\left(\frac{b_1+c_1}{2}-b_1\right)^2 +\left(\frac{b_2+c_2}{2}-b_2\right)^2\right\} \\[5pt]
\end{eqnarray}をそれぞれ展開して同じ式になることを示せばいいですね。
しかし、計算が大変ですね。もうちょっとなんとかならないでしょうか。
座標を工夫する
上のように、文字が多すぎて計算が大変になる場合は、文字を減らす工夫が大事になってきます。
中線定理に出てくるものは、線分の長さだけです。線分の長さは、三角形を平行移動したり回転したりしても、変わりません。このことを利用しましょう。
先ほど示そうとした式をもう一度見ると、一番複雑なのは波かっこの部分です。ここの計算が楽になればうれしいですね。なので、中点 M が原点に来るように平行移動してから考えましょう。
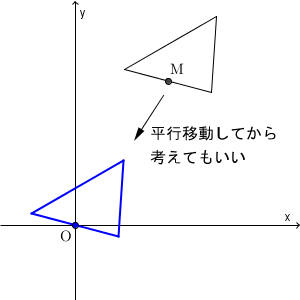
こうしても長さは変わらないので、はじめからこの状態(青い三角形の状態)で証明を開始しても構いません。 M に関する文字が消えて、計算が楽になります。
このとき、 A の座標は $(a_1,a_2)$ とおくことになりますが、 B, C は違います。というのも、この中点が原点になるように三角形を平行移動したので、 $\mathrm{ B }(b_1,b_2)$ とおくと、C の座標は $(-b_1,-b_2)$ と自然に決まります(参考:【標準】ある点に関して対称な点の座標)。 $c_1,c_2$ がいらなくなりました。
以上から、文字が6個から4個に減り、 M の座標から文字がなくなり、だいぶ計算が楽になりそうだ、ということがわかります。しかし、もう少し減らせます。
回転をしても線分の長さは変わらないので、 B, C が x 軸上に来るように回転してみましょう。
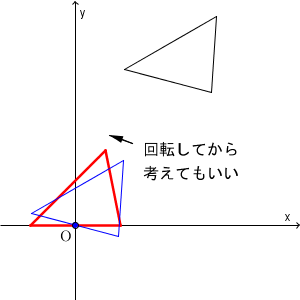
こうすれば、 B, C の y 座標からも文字がなくなり、文字は3個になりました。この状態(赤い三角形の状態)で計算してみましょう。
三角形 ABC を、 BC の中点が原点で、辺 BC が x 軸上にくるようにすると、各頂点の座標は $\mathrm{ A }(a_1,a_2)$, $\mathrm{ B }(b_1,0)$, $\mathrm{ C }(-b_1,0)$ と置くことができて、 $\mathrm{ M }(0,0)$ となります。よって、定理にある左辺は
\begin{eqnarray}
& &
\mathrm{AB}^2 +\mathrm{AC}^2 \\[5pt]
&=&
(b_1-a_1)^2+(0-a_2)^2 +(-b_1-a_1)^2+(0-a_2)^2 \\[5pt]
&=&
2a_1^2+2b_1^2+2a_2^2
\end{eqnarray}と計算でき、右辺は
\begin{eqnarray}
& &
2(\mathrm{ AM }^2 +\mathrm{ BM }^2) \\[5pt]
&=&
2 \left\{(0-a_1)^2 +(0-a_2)^2 \right\} \\
& &
+2 \left\{(0-b_1)^2 +(0-0)^2\right\} \\[5pt]
&=&
2a_1^2+2a_2^2+2b_1^2
\end{eqnarray}と変形できるので、両辺は一致します。以上から、中線定理が示せました。
はじめの状態に比べ、だいぶ計算が楽になったことがわかりますね。
おわりに
ここでは、座標を使った証明問題の例として、中線定理を示しました。
はじめは計算が大変そうに見えましたが、内容が変わらないように(今の場合なら、線分の長さが変わらないように)座標のとり方をうまく工夫することで、計算量がかなり減りました。こうした工夫は、はじめのころはなかなか思いつきにくいですが、問題を解きながらマスターしていきましょう。





