🏠 Home / 数学A / 場合の数と確率 / 組合せ

【標準】平行線と平行四辺形の個数

🕒 2017/02/17 🔄 2023/05/01

ここでは、平行な線を使って、平行四辺形がいくつできるかを数えます。平行四辺形を直接数えるのではなく、別のものを数えることで簡単に数えられるようになります。

📘 目次

平行四辺形の個数

例題1

下の図で、直線 A, B, C, D, E は互いに平行で、直線 a, b, c, d も互いに平行であるとする。このとき、この図に平行四辺形はいくつあるか、答えなさい。

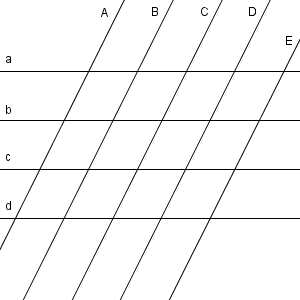
順番に数えていくなら、1x1の大きさから順番に数えていくことになるでしょう。しかし、それでは12種類の場合分けが発生するため、大変です。別の方法を考えましょう。

【標準】線や三角形の個数では、線や三角形の個数を数えるときに、「点」に注目して数えました。ここでも、別のものに対応して数えてみましょう。

次の平行四辺形を見てみましょう。

これは、直線 A, D と、直線 a, c を使ってできる平行四辺形です。このように、斜めの線を2つ選び、横の線を2つ選ぶと、それらを使って平行四辺形を作ることができます。逆に、どの平行四辺形も対応する斜めの線2本と横の線2本があります。この対応に重複や漏れはないので、平行四辺形の個数を数えることは、「斜めの線と横の線の選び方」を数えることと同じになることがわかります。

斜めの線は5本あってそこから2本選びます。横の線は4本あって2本を選びます。この選び方はそれぞれ独立して選べるので、線の選び方は\[ {}_5 \mathrm{ C }_2 \times {}_4 \mathrm{ C }_2 = 10 \times 6 = 60 \]通り、となります。よって、平行四辺形の個数は60個となります。

長方形の個数

例題2

図のように、1辺が1の正方形を、縦に3つずつ、横に4つずつ並べる。

(1) この図に長方形（正方形を含む）はいくつあるか。
(2) この図に正方形はいくつあるか。
(3) この図に長方形（正方形を除く）はいくつあるか。

(1)は、平行四辺形のときと考え方は同じです。縦の線を2本、横の線を2本選ぶことと、長方形とが対応します。縦の線が5本あって横の線が4本あるので、線の選び方の式は先ほどと同じで\[ {}_5 \mathrm{ C }_2 \times {}_4 \mathrm{ C }_2 = 10 \times 6 = 60 \]通り、となり、長方形の個数は60個となります。

(2)は、線の選び方が制限されます。2本の縦の線の間隔と2本の横の線の間隔が、同じでないといけません。そのため、単純に「組合せ」で考えることができません。

これは、直接数えてしまった方が早いです。正方形は、1辺が1か2か3しかありません。1辺が1のものは、12個あります。2のものは6個、3のものは2個です。よって、 $12+6+2=20$ 個となります。

1辺が2の正方形は、次のように考えて数えてもかまいません。横の長さが2となるような縦の線の選び方は、「左から1本目と3本目」「左から2本目と4本目」「左から3本目と5本目」の3通りの選び方があり、縦の長さが2となるような横の線の選び方は、「上から1本目と3本目」「上から2本目と4本目」の2通りの選び方があります。それぞれ、独立に選べるので $3\times 2=6$ 個と計算できます。他の長さの正方形も同様に数えることができます。

(3)は(1)から(2)を引けば終わりですね。 $60-20=40$ 個です。

ここでは、(1)(2)があったので、順番に考えることができました。しかし、(1)(2)がなく、(3)だけが出題されても同じように考えられるようにしましょう。