【標準】三次方程式の実数解の個数

🕒 2017/10/28 🔄 2023/05/01

ここでは、係数に文字を含んでいる三次方程式が、異なる実数解をいくつもつかを求める問題を見ていきます。

📘 目次

三次方程式の実数解の個数

例題

k を実数の定数とするとき、方程式 $x^3-6x^2+9x-k=0$ の異なる実数解の個数を求めなさい。

解がいくつあるかを直接考えるのは難しいですね。二次方程式の場合は、判別式を使えば解の個数がわかりますが、三次方程式の場合は判別式を使いません。

それではどうするかというと、関数に置き換えて考えるようにします。つまり、 $y=x^3-6x^2+9x-k$ が x 軸といくつ共有点を持つか、を考えるわけです。この関数が $0$ になるときを調べる、ということですね。関数を微分すれば、極大・極小がわかり、グラフの形が分かるため、 x 軸との共有点の数もわかる、という流れです。

ただ、もう少し工夫する余地があります。というのも、 $y=x^3-6x^2+9x-k$ とおくと、 k が動くたびに、このグラフは上下に動いてしまいます。そうすると、 x 軸との共有点を考えるのがやっかいになります。

そこで、もとの方程式を次のように変形します。\[ x^3-6x^2+9x=k \]このようにして、関数 $y=x^3-6x^2-9x$ のグラフと $y=k$ のグラフの共有点の数を調べる、というようにします。こうすると、1つ目の関数は、 k が含まれていないので、グラフは固定されます。また、 $y=k$ のほうも、 k が動いたときに、直線が上下するだけなので扱いやすくなります。三次関数のグラフが上下することを考えれば、だいぶスッキリしますね。

ここまでを踏まえて、関数 $y=x^3-6x^2+9x$ のグラフをかいてみましょう。

この関数を微分すると
\begin{eqnarray} y' &=& 3x^2-12x+9 \\[5pt] &=& 3(x^2-4x+3) \\[5pt] &=& 3(x-1)(x-3) \\[5pt] \end{eqnarray}となります。このことから、 $y'=0$ のとき、 $x=1,3$ となるので、増減表は次のようになります。 \begin{array}{c|ccccc} x & \cdots & 1 & \cdots & 3 & \cdots \\ \hline y' & + & 0 & – & 0 & + \\ \hline y & \nearrow & 4 & \searrow & 0 & \nearrow \end{array}よって、グラフは次のようになります。

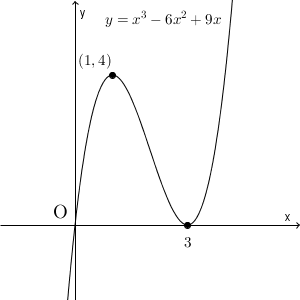
これと、 $y=k$ との共有点を考えましょう。 $k\gt 4$ のときは共有点は1点ですが、 $k=4$ のときには共有点は2点になりますね。そして、それより小さいと、しばらくの間、共有点は3点となります。

さらに進むと、 $k=0$ のときに再び共有点は2点となり、それより小さい場合は共有点は1点となります。

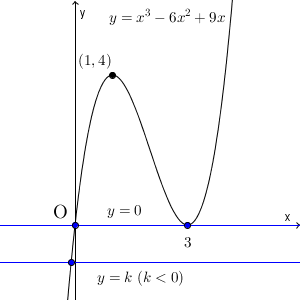
以上から、共有点の数は k によって変わります。異なる実数解の個数も同様です。なので、場合分けをして答えることになります。異なる実数解の個数は、

$k\lt 0$ または $k\gt 4$ のときは、1個
$k=0,4$ のときは、2個
$0\lt k \lt 4$ のときは、3個

となる、というのが答えです。

ここでは、係数（定数項）に文字が含まれていましたが、文字が含まれていない場合も、同じようにグラフをかいて考えることになります。例えば、「 $x^3-6x^2+9x-2=0$ は、異なる実数解をいくつ持つか」というような問題であれば、関数 $y=x^3-6x^2+9x-2$ のグラフが x 軸といくつ共有点を持つかを調べることで、求めるようにします。もちろん、上の解答から、3個であることがわかります。

このように、「グラフをかけ」と言われていなくても、増減表をかいて、グラフをかいて考える問題は出てきます。