【標準】補集合の要素の個数

🕒 2017/01/21 🔄 2023/05/01

ここでは、「Aでない、または、Bでない」などという形の集合の要素を数える問題を見ていきます。「〇〇でない」という形の条件のときは補集合を数えると考えやすくなるので、その発想で解いていきます。【基本】補集合の要素の個数も参考にしましょう。

📘 目次

かつ・またはの補集合を考えて数える

例題

1から100までの整数のうち、次のような数はいくつあるか答えなさい。
(1) 3の倍数でない、または、5の倍数でないもの
(2) 3の倍数でも5の倍数でもないもの

【基本】補集合の要素の個数で見たように、「倍数でないもの」の個数を求めるには、補集合を使って解く、つまり、全体から「倍数」の個数を引いたほうが求めやすいんでしたね。ここでも、補集合を使って考えてみましょう。

ベン図を使って、次のように3の倍数と5の倍数の集合を円を使って表します。

(1)の「3で割り切れない、または、5で割り切れないもの」というのが、どこを表すかを考えてみます。「3で割り切れない」とは、左の円に入らないということですね。そして、「5で割り切れない」とは、「右の円に入らない」ということです。つまり、「3で割り切れない、または、5で割り切れないもの」というのは、「左の円以外か、右の円以外」という部分になります。どちらかの円に入らない部分なので、次の色のついた部分に対応します。

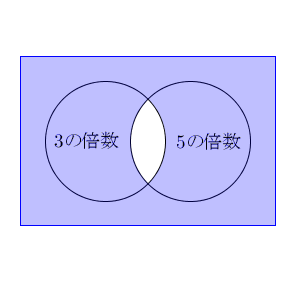
この図からわかる通り、「全体から白い部分を引く」方法で簡単に求められそうですね。白い部分は、3の倍数でも5の倍数でもあるもの、つまり、15の倍数の集合です。 $100\div 15=6.\cdots$ なので、この集合の要素の数は6個です。よって、求める個数は\[ 100-6=94 \]個となります。

ここで考えたことを、集合の観点から考え直してみましょう。【基本】条件「かつ」「または」の否定で見たように、集合については次の式が成り立ちます。\[ \overline{A\cap B} = \overline{A} \cup \overline{B} \]ド・モルガンの法則です。 A を3の倍数の集合、 B を5の倍数の集合とすると、上の式の右辺は「3の倍数でない、または、5の倍数でない」という内容になります。例題の内容ですね。一方、右辺は「『3の倍数かつ5の倍数』ではないもの」となります。上での計算は、これを考えていたんですね。

「倍数でない」ものを数えるのは大変ですが、「倍数であるもの」を数えるのは簡単です（割り算をすれば求められるので）。なので、「倍数」を数えて解けるように変形して考えたわけです。

かつ・またはの補集合を考えて数える2

続いて、2つ目の例題を考えてみましょう。「3の倍数でも5の倍数でもないもの」です。ベン図で考えると、「どちらの円にも入らないもの」なので、次の色のついた部分になります。

これも、やはり、反対サイドを考えてみます。白い部分を考えてみましょう。

白い部分は、「3の倍数」と「5の倍数」を合わせ、2回数えている部分「15の倍数」を引けば求められますね。 $100\div3=33.\cdots$, $100\div5=20$ なので、白い部分の集合の要素の個数は\[ 33+20-6=47 \]となります。よって、例題の答えは\[ 100-47=53 \]個となります。

これも、集合の観点から考えてみます。ド・モルガンの法則には、上で挙げた式以外に次の式もあります（参考：【基本】条件「かつ」「または」の否定#ド・モルガンの法則）。\[ \overline{A\cup B} = \overline{A} \cap \overline{B} \]先ほどと同様に、 A を3の倍数の集合、 B を5の倍数の集合とすると、この式の右辺が例題の内容です。これを左辺に変形したのが、上の解き方です。

ただ、例題(1)と違って、もう少し状況は複雑です。 $A\cup B$ の要素の個数を求めるには、【基本】和集合の要素の個数で見たように、次のように変形すると計算しやすくなります。\[ n(A\cup B) = n(A) +n(B) -n(A\cap B) \]左辺を求めるのは大変ですが、右辺の各項は割り算で求められます。これを計算して、全体集合の要素数から引いて求めているんですね。

【基本】条件「かつ」「または」の否定#ド・モルガンの法則で見た内容が、背景に使われています。