【標準】対数関数と最大・最小
ここでは、対数関数を含む関数の最大値や最小値を求める問題を見ていきます。
対数関数を含む関数の最大・最小
対数同士の積を、きれいに変形することはできません。対数の和は\[ \log_a M+\log_a N=\log_a MN \]と変形できますが、対数の積を真数の積にするような変形はできないので注意しましょう。
ただ、この式をそのまま眺めていても、最大値・最小値を求めることは難しいですね。これは、1つ目の対数を分解してみると、道が開けてきます。
\begin{eqnarray}
\log_2 4x
&=&
\log_2 4+\log_2 x \\[5pt]
&=&
2+\log_2 x
\end{eqnarray}こうすると、 $\log_2 x$ を別の文字で置けば、うまくいきそうだ、ということが予想できます。
$t=\log_2 x$ と置くことにしましょう。まず、こう置いたときに、 $t$ がどのような範囲をとるのかを考えましょう。 $\dfrac{1}{4}\leqq x \leqq 2$ であり、底が $1$ より大きいため、\[ \log_2 \frac{1}{4}\leqq \log_2 x \leqq \log_2 2 \]となります。このことから、\[ -2\leqq t \leqq 1 \]が $t$ のとる範囲であることがわかります。
さて、この範囲で、もとの関数が取りうる値の範囲を考えましょう。もとの関数を $t$ で表すと
\begin{eqnarray}
y
&=&
(\log_2 4x)(\log_2 x) \\[5pt]
&=&
(2+\log_2 x)(\log_2 x) \\[5pt]
&=&
(2+t)\times t \\[5pt]
&=&
t^2+2t \\[5pt]
&=&
(t+1)^2-1 \\[5pt]
\end{eqnarray}となります。 $-2\leqq t \leqq 1$ であることに注意してグラフをかくと、次のようになります。

このことから、 $t=-1$ のときに最小値 $-1$ をとり、 $t=1$ のときに最大値 $3$ をとることがわかります。
もともと $\log_2 x=t$ と置いていたので、 $x=2^t$ です。よって、 $x=\dfrac{1}{2}$ のときに最小値 $-1$ をとり、 $x=2$ のときに最大値 $3$ をとることがわかります。これが答えです。
ちなみに、 $t=\log_2 x$ と置かずに、 $y=(\log_2 4x)(\log_2 x)$ のグラフをかくと、次のようになります。
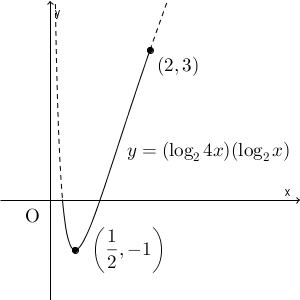
現時点での学習内容では、このグラフをかくことはできませんが、将来、対数関数の微分を学べばかけるようになります。
おわりに
ここでは、対数関数を含む関数の最大値・最小値を求める問題を見ました。対数関数を別の文字で置く場合、新しい文字の取りうる範囲に注意しましょう。そのとき、底が $1$ より大きいか小さいかを確認することを忘れないようにしましょう。
対数関数を別の文字で置くときには、その前に式変形を行わないといけないこともあります。\[ \log_a M+\log_a N=\log_a MN \]などの性質を、左から右へだけでなく、右から左へ変形するために使うこともあります。同じ対数関数が出てくるように、うまく変形しましょう。





