【標準】楕円の焦点

🕒 2018/04/15 🔄 2023/05/01

ここでは、楕円の方程式から焦点を求める問題を見ていきます。

📘 目次

楕円の方程式から焦点を求める

【基本】楕円の焦点（焦点がx軸上）で見た通り、 $a\gt b \gt 0$ のときに、 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ のグラフは、 $(-\sqrt{a^2-b^2},0)$, $(\sqrt{a^2-b^2},0)$ の2点を焦点とする楕円となります。これを踏まえて、次のような問題が出題されることがあります。

例題

楕円 $x^2+4y^2=4$ の焦点の座標を求めなさい。

【基本】楕円の方程式と円の方程式で見たように、この式は、円の方程式 $x^2+y^2=4$ とよく似ていますね。 $x^2,y^2$ の係数が両方とも正で、違う値なので、楕円の方程式であることがわかります。

この焦点の座標ですが、冒頭で見た対応がわかりやすくなるように、右辺が $1$ になるように変形しましょう。\[ \dfrac{x^2}{4}+y^2=1 \]これより、冒頭の式の $a=2,b=1$ のときであることがわかるので、焦点の座標は $(-\sqrt{3},0)$, $(\sqrt{3},0)$ であることがわかります。

この対応を忘れてしまっていても、図をかいて、特別な点を元に考えれば、焦点の座標を出すことはできます。楕円の方程式からすぐに4つの通る点がわかりますね。 $(2,0)$, $(-2,0)$, $(0,1)$, $(0,-1)$ です。これをもとに楕円をかいてみます。

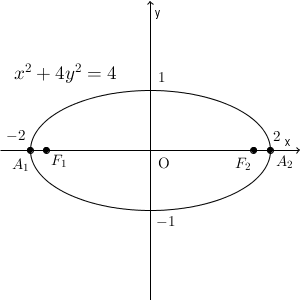
まず、 $A_2(2,0)$ と2つの焦点 $F_1,F_2$ との距離の和を考えてみます。焦点の場所がわからなくても、図が $y$ 軸について対称であることから、\[ F_1A_2+F_2A_2=F_1A_2+F_1A_1=A_1A_2 \]となるので、2つの焦点からの距離の和は $4$ であることがわかります。

楕円は、「2つの焦点からの距離の和が等しい点の軌跡」だったので、他の点についても距離の和は $4$ になります。続いて、 $(1,0)$ について考えましょう。

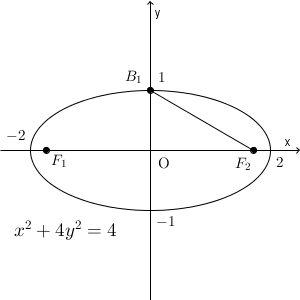
三角形 $OB_1F_2$ について考えましょう。 $OB_1=1$ です。また、 $F_1B_1+B_1F_2=4$ だったので、 $B_1F_2=2$ ですね。よって、 $OF_2=\sqrt{2^2-1^2}=\sqrt{3}$ となります。以上から、2つの焦点の座標は、 $(-\sqrt{3},0)$, $(\sqrt{3},0)$ と求められます。

方程式の係数と焦点の座標の関係を忘れてしまっても、図をかいて思い出すことができます。【基本】楕円の焦点（焦点がy軸上）でも、後半で似ている話を載せています。ただ、これは、思い出すためのテクニックなので、答案に書くのはやめておきましょう。

焦点から楕円の方程式を求める

焦点から、楕円の方程式を求める場面（楕円となること自体の説明が不要な場面）もありえます。

例題

2点 $(0,\sqrt{7})$, $(0,-\sqrt{7})$ を焦点とし、焦点からの距離の和が $8$ となる楕円の方程式を求めなさい。

問題文から、楕円になること自体の説明は不要だと考えられます。方程式を求めるだけですね。

先ほどの例題と同じような図をかけば、「焦点からの距離の和」と「長軸の長さ」が同じことがわかります。また、長軸は、2つの焦点を結んだ直線の上にあるので、まず、この楕円は $(0,4)$, $(0,-4)$ を通ることがわかります。

一般的には、この後は、焦点の座標が $(0,\pm\sqrt{b^2-a^2})$ とかけることから、 $a$ を求める、という流れになります。もし、係数と焦点の座標との対応を忘れてしまった場合は、次のようにします。

先ほどの例題と同じように、原点、焦点、短軸の端点を結んだ直角三角形を考えます。 $(a,0)$ も通るとすると、\[ \sqrt{a^2+7}=4^2 \] なので、 $a=\pm3$ となります。よって、この楕円の頂点は、 $(0,4)$, $(0,-4)$, $(3,0)$, $(-3,0)$ なので、この楕円の方程式は\[ \dfrac{x^2}{9}+\dfrac{y^2}{16} =1 \]となることがわかります。