【標準】連続性から係数を求める

ここでは、ある関数が連続関数となるように係数を決める、という問題を見ていきます。

連続性から係数を求める

【標準】関数の連続性では、関数が連続かどうかを見ましたが、今回は連続になるように係数を決める、という問題です。この関数を見て、すぐに連続かどうかはよくわかりません。まずは、極限を考えてから、「連続」の部分について考えていくことにします。 $x^n$ の極限がどうなるかは $x$ の値によって変わるため、リンク先と同じように $x$ の値で場合分けをして考えていきます。

まず、 $|x|\lt 1$ の場合を考えましょう。このとき、 $n\to\infty$ とすると、 $x^{2n}$ も $x^{2n+1}$ も $0$ に収束します。よって、このときは\[ f(x)=\frac{0+ax^2+bx}{0+1}=ax^2+bx \]となります。

$|x|\gt 1$ の場合は、分母も分子も発散します。こういう場合、【基本】分数関数の極限で見たように、分母分子を同じもので割ると極限が求められる場合があります。今の場合は、 $x^{2n}$ で割ると
\begin{eqnarray} f(x) &=& \lim_{n\to \infty} \frac{x^{2n-1}+ax^2+bx}{x^{2n}+1} \\[5pt] &=& \lim_{n\to \infty} \frac{\frac{1}{x}+\frac{ax^2}{x^{2n} }+\frac{bx}{x^{2n} }}{1+\frac{1}{x^{2n} }} \\[5pt] &=& \frac{\frac{1}{x}+0+0}{1+0} \\[5pt] &=& \frac{1}{x} \end{eqnarray}となります。

他は、 $x=\pm 1$ のときですね。これらはそのまま代入して値を求めることができます。 $x=1$ のときは\[ f(1)=\frac{1+a+b}{1+1}=\frac{a+b+1}{2} \]となります。 $x=-1$ のときは、 $x^{2n}=1$ で、 $x^{2n-1}=-1$ なので、\[ f(x)=\frac{-1+a-b}{1+1}=\frac{a-b-1}{2} \]となります。

以上から、 $|x|\lt 1$ の部分では $f(x)=ax^2+bx$ 、 $|x|\gt 1$ の部分では $f(x)=\dfrac{1}{x}$ なので、これらの区間では連続であることがわかります。問題は $x=1,-1$ のところです。ここで連続なら、全体で連続となります。

$x\gt 1$ のときは $f(x)=ax^2+bx$ なので、 $x\to 1+0$ とすると $f(x)\to a+b$ となります。また、 $x\to 1-0$ のときは $f(x)\to 1$ となります。また、 $f(1)=\dfrac{a+b+1}{2}$ なので、 $x=1$ で連続となるには、 $a+b=1$ かつ $\dfrac{a+b+1}{2}=1$ を満たさなくてはいけません。1つ目の式が成り立てば2つ目の式は成り立つので、 $x=1$ で連続になるための条件は\[ a+b=1 \]となります。

次に、 $x=-1$ での連続性について考えます。 $x\to -1+0$ とすると、 $f(x)\to a-b$ となります。 $x\to -1-0$ とすると $f(x)\to -1$ となります。 $f(-1)=\dfrac{a-b-1}{2}$ なので、 $x=-1$ で連続となるには、 $a-b=-1$ かつ $\dfrac{a-b-1}{2}=-1$ を満たさなくてはいけません。1つ目が成り立てば2つ目は成り立つので、 $x=-1$ で連続になるための条件は\[ a-b=-1 \]となります。

2つの式 $a+b=1$, $a-b=-1$ の両辺同士を足すと $a=0$ が得られ、これから $b=1$ が得られます。これらが答えです。

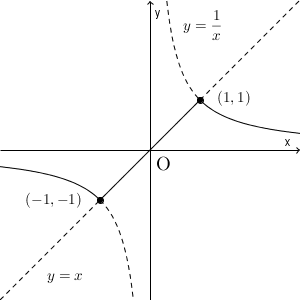
$a=0$, $b=1$ とすると、 $x=\pm 1$ で連続となり、 $f(x)$ は連続関数となります。 $y=f(x)$ のグラフをかけば次のようになります。

おわりに

ここでは、関数が連続となるように、関数の係数を決める問題を見てきました。通常は、境目となる部分（上の例題であれば、 $x\pm 1$ の箇所）での連続性を考えることになります。この境目は、等比級数や無限等比級数がいつ収束していつ発散するか、という境目に対応することが多いので、これらの内容も復習しておきましょう（参考：【基本】等比数列の極限、【基本】無限等比級数）。