【標準】円に内接する四角形

🕒 2022/08/27 🔄 2023/05/01

ここでは、円に内接する四角形に関する問題を見ていきます。

📘 目次

例題

次の図のように、 $\triangle \mathrm{ABC}$ の辺上に点 $\mathrm{P,Q,R}$ をとったところ、 $\mathrm{AP}\perp \mathrm{BC}$, $\mathrm{PQ}\perp \mathrm{CA}$, $\mathrm{PR}\perp \mathrm{AB}$ となりました。以下の問いに答えなさい。

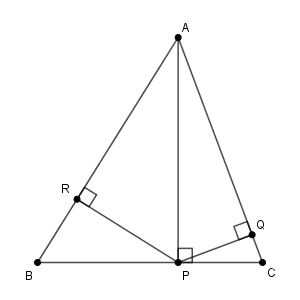
(1) 4点 $\mathrm{A, P, Q, R}$ が同一円周上にあることを示しなさい。
(2) 4点 $\mathrm{B, C, Q, R}$ が同一円周上にあることを示しなさい。

図には円の姿はまったく見えないですが、円に関することが示せるのは少し不思議ですね。考えていきましょう。

4点が同一円周上にあることを示すには、【基本】四角形が円に内接するための条件で見たように、「対角の和が $180^{\circ}$ 」などを示す方法があります。

今の場合、(1)ではまさにこれが使えて、\[ \angle \mathrm{ARP}+\angle \mathrm{AQP}=90^{\circ}+90^{\circ}=180^{\circ} \]なので、四角形 $\mathrm{ARPQ}$ が円に内接すること、4点 $\mathrm{A, P, Q, R}$ が同一円周上にあることがいえます。

例題の続き

例題

(1) 4点 $\mathrm{A, P, Q, R}$ が同一円周上にあることを示しなさい。
(2) 4点 $\mathrm{B, C, Q, R}$ が同一円周上にあることを示しなさい。

次に(2)を示しましょう。先ほどと違って、少し考えにくくなっています。

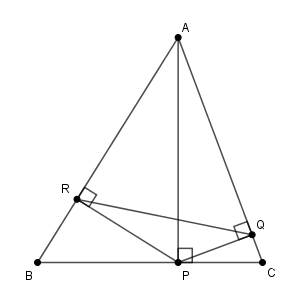
四角形 $\mathrm{BCQR}$ で考えると、 $\angle \mathrm{B}$ の対角の外角は $\angle \mathrm{AQR}$ です。これが $\angle \mathrm{B}$ と等しいことがいえればいいですが、すぐにはいえそうにありません。

しかし、先ほど示した(1)を使うとどうでしょうか。わかりやすいように、円を追加して考えてみましょう。

こうすると、 $\angle \mathrm{AQR}$ は、円周角の定理から $\angle \mathrm{APR}$ と等しいことがわかります。ここで、 $\triangle \mathrm{ABP}$ と $\triangle \mathrm{APR}$ について考えると、示したいことが示せますね。

まとめると、次のようになります。

\begin{array}{llll} & & \angle \mathrm{AQR} & \\ &=& \angle \mathrm{APR} & (\textsf {(1)と円周角の定理より} ) \\ &=& 90^{\circ}-\angle \mathrm{PAR} & (\triangle \mathrm{APR} \textsf{に着目}) \\ &=& \angle \mathrm{B} & (\triangle \mathrm{ABP} \textsf{に着目} ) \end{array}

こうして、 $\angle \mathrm{B}$ は、対角の外角 $\angle \mathrm{AQR}$ と等しいことがわかるので、4点 $\mathrm{B, C, Q, R}$ が同一円周上にあることが示せました。