【標準】三次式の因数分解と体積

🕒 2017/04/14 🔄 2023/07/13

ここでは、三次式の展開や三次式の因数分解で出てきた公式を、体積とからめてみていきます。テストや入試で出るような内容ではありませんが、「式の内容を図形で見るとこうなる」というのがわかり、理解が深まると思います。

📘 目次

3乗の公式

まずは、次の3乗の公式について考えてみます。\[ (x+y)^3 = x^3 +3x^2y +3xy^2 +y^3 \]左辺を図形的なものとしてとらえると、「一辺が $x+y$ の立方体の体積」と考えることができます。

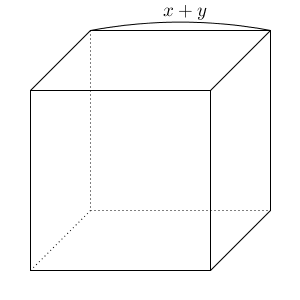
一方、右辺を見ると、 $x^3$ や $y^3$ が出てくることから、一辺が x や y の立方体が出てくるように、次のように分解してみます。

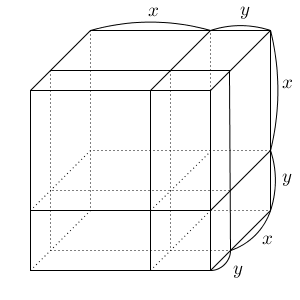
このように切断すると、まず左上奥に、一辺が x の立方体が出てきます。

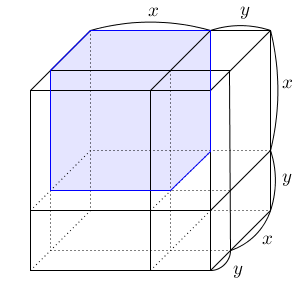
この立方体の体積は $x^3$ ですね。

次に、大きな直方体について考えてみましょう。

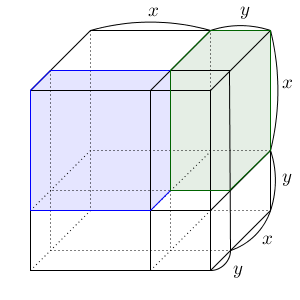
手前左側と、右上奥に、同じ直方体がありますね。左下の奥にも、もう1つあります。

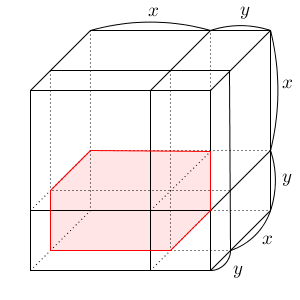
これらは、辺の長さが x, x, y の直方体です。なのでこの3つの直方体の体積をあわせれば $3x^2y$ となります。

続いて、細長い直方体について考えてみましょう。

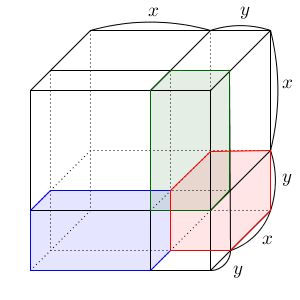
手前左下、手前右上、右下奥の3か所に、同じ直方体があります。これらは、辺の長さが x, y, y の直方体です。なので、この3つの直方体の体積の合計は $3xy^2$ となります。

最後は、手前右下の小さな立方体です。

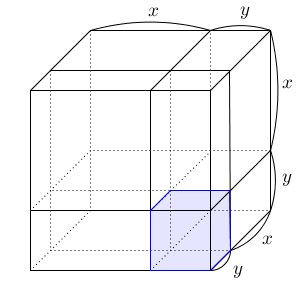
ここの体積は、 $y^3$ です。

分解前の体積と分解後の体積は同じです。分解してできるものは、大きな立方体、3つの大きな直方体、3つの細長い直方体、小さな立方体を合わせたものなので、体積は\[ x^3 +3x^2y+3xy^2+y^3 \]となります。これが分解前の体積 $(x+y)^3$ と同じになります。これはまさしく、3乗の展開・因数分解の公式そのものですね。

こうして、3乗の展開・因数分解の公式は、立方体の分割で考えることができることがわかりました。

3乗引く3乗の公式

続いて、3乗引く3乗の公式について考えてみましょう。\[ x^3-y^3 = (x-y)(x^2+xy+y^2) \]左辺を見ると、一辺が x の立方体、一辺が y の立方体の体積を考えればよさそうです。上と似たような図ですが、次のような図形を考えてみます。

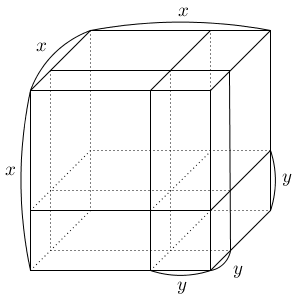
先ほどの図と違うところは、一辺が x になっているところです。また、因数分解をする前の式は、全体の立方体から、手前右下にある小さな立方体を取り除いた図形の体積になっている点に注意しましょう。

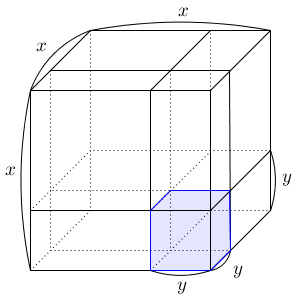
さて、全体の立方体から、手前右下にある小さな立方体を取り除いた図形を、3つに分解してみます。まずは、奥にある大きな直方体に注目しましょう。

この直方体は、横の長さが $x$ で、奥行きが $x-y$ で、高さが $x$ です。なので、この体積は\[ (x-y) \times x^2 \]と書くことができます。

続いて、手前上側にある直方体を見てみましょう。

この直方体は、横の長さが $x$ で、奥行きが $y$ で、高さが $x-y$ です。なので、この体積は\[ (x-y) \times xy \]と書くことができます。

最後に、手前下側にある直方体を考えましょう。

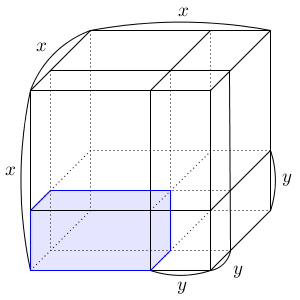
この直方体は、横の長さが $x-y$ で、奥行きが $y$ で、高さが $y$ です。なので、この体積は\[ (x-y) \times y^2 \]と書くことができます。

全体の立方体から小さい立方体を引くと考えると、体積は $x^3-y^3$ と書くことができます。一方、3つの直方体に分解したと考えると、上で考えた3つの体積を足したものになるので
\begin{eqnarray} & & (x-y) \times x^2 + (x-y) \times xy + (x-y) \times y^2 \\ &=& (x-y) (x^2+xy+y^2) \end{eqnarray}となります。分解の仕方で体積は変わらないので、この2つの式は同じなります。これは展開・因数分解の公式そのものですね。

こうして、「3乗引く3乗」の展開・因数分解の公式も、立方体の分割で考えることができることがわかりました。