【標準】積分を使って体積を求める

🕒 2023/07/16

ここでは、積分を使って体積を求める問題を解いていきます。

📘 目次

例題

下の図のように、底面の半径が $a$ で高さが $a$ より高い円柱があります。ここで、底面の直径を含み、底面と $45^{\circ}$ の角をなす平面でこの円柱を切断し、2つの立体に分けます。このとき、小さい方の立体の体積を求めなさい。

赤い線で切って、右下にある立体の体積を求める、という問題です。円柱でも円すいでもないので、今までの知識だと体積を求めることはできませんでしたが、積分を使えば求められるようになります。

【基本】積分を使って体積を求めるで見たように、断面を積分すればいいのでした。しかし、今の場合、どのように立体を切断すればいいのでしょうか。あとで積分することも踏まえて考えてみます。

まず、1つのやり方として、 $x$ 軸に垂直な平面で切る、という方法があります。

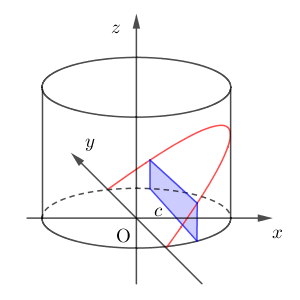
平面 $x=c$ で切ったとしましょう。 $0\leqq c\leqq a$ です。このように切断すると、断面は青い部分のようになります。長方形ですね。

底面は円であり、この円の方程式は $x^2+y^2=a^2$ なので、切り口の長方形の下の辺の長さは\[ 2\sqrt{a^2-c^2} \]となります。長方形の縦の長さは、立体を切ったときの平面が底面と $45^{\circ}$ をなすという条件から、 $c$ だとわかります。

こうして、断面積は\[ 2c\sqrt{a^2-c^2} \]となることがわかります。よって、体積は、 $c$ を $x$ に置き換えて、 $x$ について積分すればいいので\[ \int_0^a 2x\sqrt{a^2-x^2}dx \]となります。

$t=a^2-x^2$ とすると、 $dt=-2xdx$ だとわかります。また、 $x$ が $0\to a$ と変化するとき、 $a^2 \to 0$ なので、置換積分をすると次のようになります。
\begin{eqnarray} & & \int_0^a 2x\sqrt{a^2-x^2}dx \\[5pt] &=& \int_{a^2}^0 \sqrt{t} (-1)dt \\[5pt] &=& \int_0^{a^2} \sqrt{t} dt \\[5pt] &=& \left[\frac{2 t\sqrt{t}}{3}\right]_0^{a^2} \\[5pt] &=& \frac{2}{3}a^3 \\[5pt] \end{eqnarray}と求められます。

これで答えが求められましたが、この問題は別の方法で求めることもできます。

別解

例題

先ほどは $x$ 軸について垂直な平面で切りました。しかし、切り方は他にも考えられます。 $y$ 軸について垂直な平面で切る、という方法もあるでしょう。 $y=c$ で切ったとしましょう（ $-a\leqq c \leqq a$ とします）。

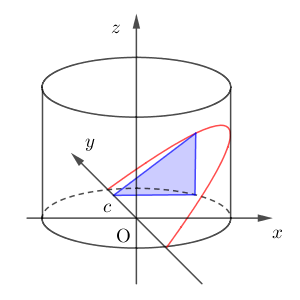
今回は、切り口は直角二等辺三角形です（図が悪くてあまりそうは見えませんが）。この下の辺の長さ、つまり、直角の部分の $x$ 座標は、 $y$ 座標が $c$ であることを使うと\[ \sqrt{a^2-c^2} \]だとわかります。

なので、断面の面積は\[ \frac{a^2-c^2}{2} \]です。よって、この式の $c$ を $y$ で積分すれば、答えがわかります。今回は $y$ 軸について動かすので、 $y$ で積分します。

\begin{eqnarray} & & \int_{-a}^a \frac{a^2-y^2}{2}dy \\[5pt] &=& 2\int_0^a \frac{a^2-y^2}{2}dy \\[5pt] &=& 2 \left[\frac{a^2}{2}y-\frac{y^3}{6}\right]_0^a \\[5pt] &=& \frac{2}{3}a^3 \end{eqnarray}となります。

なお、図形を90度回転させて $x$ について積分する、とやってもかまいません。

2つの方法で解きましたが、後半のほうがかなり計算が楽になりましたね。このように、立体の体積を求める問題では、どのように切るかによって、その後の計算の難易度が大きく変わってくることがあります。いろんな切り方を考えたり、積分の計算を練習する必要があります。