【標準】箱ひげ図

【基本】箱ひげ図で箱ひげ図の紹介をしました。試験では、箱ひげ図をかかないといけない場面はほとんどなく、選択肢の中から適切な箱ひげ図を選ぶ問題のほうが多いです。

ここでは、ヒストグラムと矛盾しない箱ひげ図を選ぶ問題を考えてみます。

まずは最大値・最小値を見る

ある20人のクラスで、50点満点のテストをしたとします。次のグラフは、そのテスト結果のヒストグラムです。

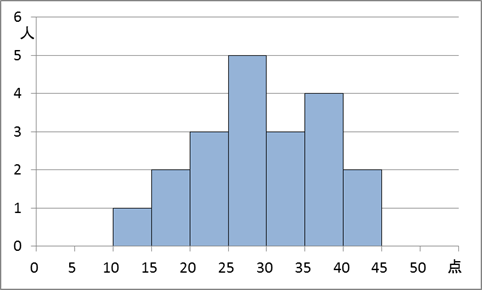
ここで、10と15の間にある1人は、「10点以上15点未満の人が1人であった」ことを表すものとします。

このとき、次の6つの箱ひげ図のうち、上のヒストグラムと矛盾しないものはどれか、考えてみましょう。

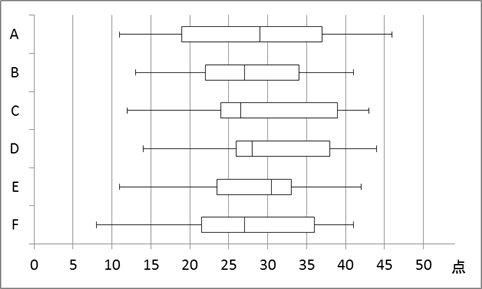
箱ひげ図が何を表しているかが不安な人は、【基本】箱ひげ図を見てみましょう。

まずは、すぐにわかる最小値・最大値を見るのがいいでしょう。ヒストグラムを見ると、一番点数の低い人は「10点以上15点未満」であることがわかります。なので、箱ひげ図の左端が5と10の間にあるＦは間違いであることがわかります。また、一番点数の高い人は「40点以上45点未満」なので、Ａがおかしいことがわかります。

ここでは2つの選択肢が消えました。ただ、実際の試験では、最大値・最小値だけを見て選択肢が消えるような簡単な問題が出ることは少ないです。

四分位数を出す

続いて、箱ひげ図の箱の部分を考えていきます。箱の部分は、第1四分位数、中央値、第3四分位数を表しているんでしたね。

これらの値は、ヒストグラムを見てもすぐにはわかりません。こういう場合は、ヒストグラムのどの部分にあるか、直接求めてみます。

人数が20人なので、中央値は「下から10番目と11番目の平均」です。次のように、下から順位をつけて行ってみましょう。

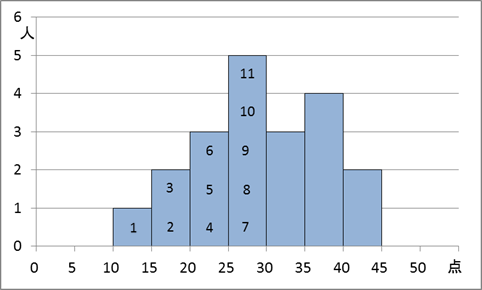
これからわかる通り、下から10番目も下から11番目も、「25点以上30点未満」であることがわかります。この2つの平均が中央値なので、中央値もこの範囲にあることがわかります。Ｅを見ると、箱の中央にある線が「25点以上30点未満」の範囲外にあるので、不適切であることがわかります。

第1四分位数は、下位10人の中央値なので、下から5番目と6番目の平均ですね。先ほどつけた順位を見るとわかりますが、第1四分位数は「20点以上25点未満」であることがわかり、ＡとＤが矛盾していることがわかります。

第3四分位数は、上位10人の中央値です。同じように順位を書いていくと、「35点以上40点未満」になることがわかるため、ＢとＥが矛盾することがわかります。

このように、不適切な選択肢を消去していくと、ヒストグラムと矛盾しない選択肢はＣしかないことがわかります。これが答えとなります。

おわりに

ここでは、箱ひげ図に関する典型的な問題の解き方を見ました。データ数が少ない場合は、ヒストグラムから直接四分位数を読み取って解くようにしましょう。