【基本】外れ値

🕒 2022/07/15 🔄 2023/05/01

ここでは、データの中に含まれた極端な値、外れ値について見ていきます。

📘 目次

外れ値

夏の高校野球を見たことがある人は多いでしょう。それぞれの試合で、だいたい何点差で勝負がついたかを調べたとしましょう。

そんなに詳しく見たことがない人でも、ほとんどが1点差や2点差で、10点以上も差がつくことはほとんどない、と予想するでしょう。

ところが、地方大会だと、ごくまれにとんでもない差が生まれることがあります。

1つ目の記事は122点差、2つ目の記事は82点差です。こんな差がつくこともあるんですね。

データを分析する際、他の値から極端に離れた値が含まれることがあります。このような値を 外れ値 といいます。上の例でいえば、122点や82点は外れ値と言えるでしょう。

「外れ値は、極端に離れた値だ」と書きましたが、極端に離れているかどうかはどのように判定するのでしょうか。データにはいろいろな種類があるので、「このようにすれば、必ずOK」というものはないのですが、いくつか標準的な手法はあります。

一つは、四分位数を利用する方法です。以下に該当するものを外れ値とします。

これは、John Tukeyという数学者が提唱した手法です。

箱ひげ図を使っている場合、次のように、箱ひげ図に外れ値を反映させることがあります。

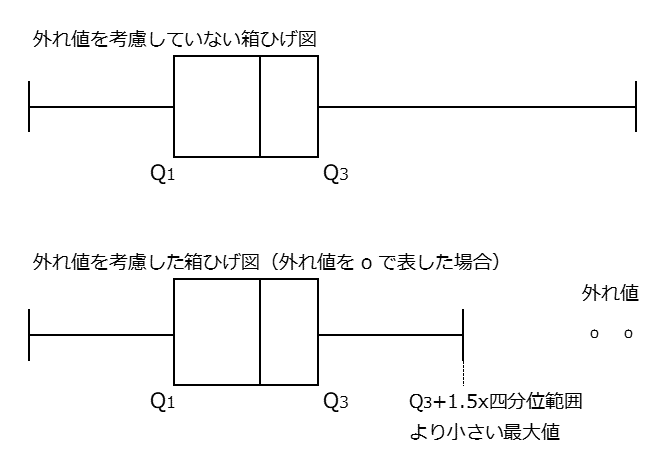
外れ値は o や x で表し、最大値や最小値は外れ値を除いたものにします。また、四分位範囲や中央値はそのまま（外れ値を除く前と同じ）で作成します。上の例は、外れ値が2つあることを表しています。

また、平均と標準偏差を使った方法もあります。以下に該当するものを外れ値とします。

平均から標準偏差の3倍以上離れているものを外れ値とする、という方法です。この場合、極端に大きな値が平均にも影響を与えている点に注意が必要です。また、値の数が十分多くないといけません。

外れ値がある場合、まずは なぜ外れ値が発生したのかを調べること が重要です。

例えば、測定ミスや入力ミスなどが考えられます。ある測定者だけ正しい方法で測定していなかった、入力するときに単位を間違っていた、手書きの0を6と見間違えた、などがありえます。測定方法が間違っていたなどの場合は、データの信ぴょう性にかかわってくるため、再測定が必要でしょう。

測定ミスなどの原因によって値がかけ離れている場合は、外れ値ではなく「異常値」と呼ぶこともあります。一般的に、データの分析を行う際、異常値は除外します。ただし、異常値を除外した結果、値の個数が極端に少なくなってしまう場合は、再測定が必要になるかもしれません。

ミスなどが考えられない場合でも、外れ値が発生することはあります。例えば、2020年からの新型コロナ流行によって、さまざまな統計データが影響を受け、データによっては外れ値が発生しやすくなったでしょう。また、戦争や天災が発生した場合でも、その年の統計データが他の年とはかけ離れた値をとることがあります。

データの分析を行う上で、外れ値を除外すべきかどうかは、どのような分析を行うかによります。例えば、薬の副作用に関するデータであれば、たとえ小さすぎる値であっても、除外すべきではないかもしれません。目的に応じて扱い方を考える必要があります。

なお、外れ値の原因を調べることで、新しく問題を発見したり、逆に問題解決の手がかりが得られたりすることがあります。例えば、売上データを分析して外れ値が見つかった場合、その原因を調査することで、販売方法に関する問題を見つけたり、売上の改善方法のヒントが見つかるかもしれません。

外れ値はいつも悪いものというわけではないですし、いつでも除外すればいいというものでもありません。

ここでは、外れ値について見てきました。テストでは外れ値を含むデータはあまり扱わないかもしれませんが、現実の世界では扱うデータの中に外れ値が含まれることがあります。外れ値が発生する原因を調べ、分析の目的に応じてどのように取り扱うかを考えましょう。

対象者：数学I

レベル：基本

キーワード：外れ値

チャンネル登録はコチラから（以下は、動画のサンプルです）