【標準】2曲線間の面積と積分

🕒 2017/12/02 🔄 2023/05/01

ここでは、直線や曲線で囲まれた部分の面積を、積分を使って求める方法を見ていきます。【基本】2曲線間の面積と積分の具体的な計算例を見ていきます。

📘 目次

直線と放物線の間の面積

例題1

直線 $y=x+3$ と放物線 $y=2x^2-3x-3$ で囲まれた部分の面積を求めなさい。

【基本】2曲線間の面積と積分で見たように、上から下を引いて、左から右まで積分をすれば求められます。まずは、グラフをかいて考えていきましょう。

直線と放物線の交点の x 座標は
\begin{eqnarray} x+3 &=& 2x^2-3x-3 \\[5pt] 2x^2-3x-3-x-3 &=& 0 \\[5pt] 2x^2-4x-6 &=& 0 \\[5pt] 2(x-3)(x+1) &=& 0 \\[5pt] x &=& 3,-1 \\[5pt] \end{eqnarray}となります。グラフは次のようになります。

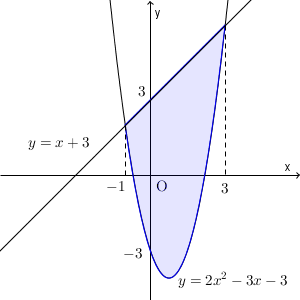
囲まれている部分では、直線の方が上になっています。このことから、次の積分を計算した答えが、求める面積となります。\[ \int_{-1}^3 \{ (x+3)-(2x^2-3x-3) \} dx \]これを計算すると
\begin{eqnarray} & & \int_{-1}^3 \{ (x+3)-(2x^2-3x-3) \} dx \\[5pt] &=& \int_{-1}^3 (-2x^2+4x+6) dx \\[5pt] &=& \left[ -\frac{2}{3}x^3+2x^2+6x \right]_{-1}^3 \\[5pt] &=& \left( -\frac{2}{3}\cdot 27+2\cdot 9+6\cdot 3 \right)-\left( \frac{2}{3}+2-6 \right) \\[5pt] &=& 18+\frac{10}{3} \\[5pt] &=& \frac{64}{3} \\[5pt] \end{eqnarray}と求めることができます。

2つの放物線の間の面積

例題2

2つの放物線 $y=x^2$, $y=-x^2-x+1$ で囲まれた部分の面積を求めなさい。

先ほどと異なり、両方とも放物線になっていますが、求め方は同じです。まずは、交点を求め、グラフをかいて、上下関係を把握します。

交点の x 座標は
\begin{eqnarray} x^2 &=& -x^2-x+1 \\[5pt] 2x^2+x-1 &=& 0 \\[5pt] (2x-1)(x+1) &=& 0 \\[5pt] x &=& \frac{1}{2},-1 \end{eqnarray}となります。グラフは次のようになります。

囲まれている部分では、 $y=-x^2-x+1$ のグラフの方が上になっています。そのため、\[ \int_{-1}^{\frac{1}{2} } \{ (-x^2-x+1)-x^2 \} dx \]を計算すればいいことがわかります。
\begin{eqnarray} & & \int_{-1}^{\frac{1}{2} } \{ (-x^2-x+1)-x^2 \} dx \\[5pt] &=& \int_{-1}^{\frac{1}{2} } (-2x^2-x+1) dx \\[5pt] &=& \left[ -\frac{2}{3}x^3-\frac{1}{2}x^2+x \right]_{-1}^{\frac{1}{2} } \\[5pt] &=& \left( -\frac{2}{3}\cdot \frac{1}{8}-\frac{1}{2}\cdot \frac{1}{4}+\frac{1}{2} \right) \\[5pt] & & -\left( \frac{2}{3}-\frac{1}{2}-1 \right) \\[5pt] &=& \left( -\frac{2}{24}-\frac{1}{8}+\frac{1}{2} \right) +\frac{5}{6} \\[5pt] &=& \frac{-2-3+12+20}{24} \\[5pt] &=& \frac{27}{24} \\[5pt] &=& \frac{9}{8} \\[5pt] \end{eqnarray}が答えとなります。