【発展】円に内接する正五角形の作図(デザインあ おとなスペシャル2020で紹介されてたやつ)
ここでは、円に内接する正五角形の作図方法について詳しく見ていきます。2020年の1月に放送された「デザインあ おとなスペシャル」でも紹介されていた作図方法ですが、ここでは辺の長さを求めるところも考えます。なお、三平方の定理以外に、余弦定理も使います。
正五角形を作図するとは?
数学で「作図」というと、定規とコンパスだけを使って図をかくことをいいます。定規は線を引くだけにしか使わず、長さを測ることはできません。コンパスは、ある点を中心とした円をかくことと、2点間の距離をとることに使えます。それ以外には使えませんし、これら以外の道具も使えません。分度器を使って角度を測るのもダメです(参考:【基本】作図で使う定規とコンパス)。
問題によっては使える道具の条件が異なることもありますが、基本はこのルールです。以下で見る正五角形の作図も、このルールで作図できます。
まだどうやって作図すればいいかはわかりませんが、初めの方の手順は次のようになります。まず、適当に点をとります。この点を O とします。点 O を中心とした円をかきます。半径は適当でいいです。
そして、うまく作図して、なんやかんやあった後、次のように円に内接する正五角形ができます。
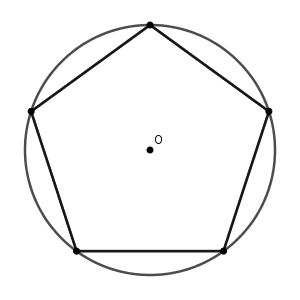
これがゴールです。定規とコンパスでここまでたどり着くことができます。以下で詳しく見ていきましょう。
正五角形の一辺の長さ
先ほどの図に点の名前をかき加えて考えてみます。時計回りに A から E と名前を付けます。
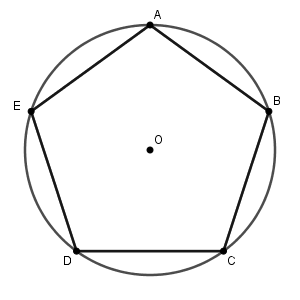
点 O は好きな場所で、半径も好きな長さでした。点 A の場所は円周上の点であればどこでもいいです。これらを決めれば、 B から E が決まります。この4点をどのようにかけばいいかがわかれば、正五角形が出来上がります。
攻め方は大きく2つ考えられます。1つは AB の長さを作図する方法。もう1つは $\angle \mathrm{ AOB }$ を作図する方法です。よく知られているのは前者の方法なので、ここでも前者の方法を考えていくことにします。
正五角形の一辺の長さを作図するには、長さがわかっていた方がいいですね。長さを測る道具が使えないので半径 OA が何cmなのかはわかりませんが、作図には必要はないので問題ありません。作図に必要なのは、 OA の長さに対して、正五角形の一辺の長さがいくらか、です。比がわかればいいんですね。そのため、以下では、 $\mathrm{ OA }=1$ として考えていきます。 OA を長さの基準にするということです。
さて、正五角形を次のように5つに分割して考えてみます。
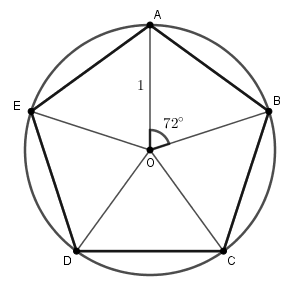
ここで、三角形 AOB に注目してみます。 $\mathrm{ OA=OB=1 }$ であり、 $\angle \mathrm{ AOB }=72^{\circ}$ です。そして、今知りたいのは AB の長さです。なので、余弦定理を使えば求められます(参考:【基本】余弦定理の基本的な使い方)。
\begin{eqnarray}
\mathrm{ AB }^2
&=&
\mathrm{ AO }^2+\mathrm{ OB }^2-2\cdot \mathrm{ AO }\cdot \mathrm{ OB }\cdot \cos \angle \mathrm{ AOB } \\[5pt]
&=&
1+1-2\cdot 1\cdot 1\cdot \cos 72^{\circ} \\[5pt]
&=&
2-2\cos 72^{\circ} \\[5pt]
\end{eqnarray}となります。
ここでまた新しい分からないもの $\cos 72^{\circ}$ が出てきました。次は、この値を求めてみましょう。
72度のcos
さて、円に内接する正五角形の作図を考える上で、半径が $1$ なら正五角形の一辺の長さが $2-2\cos 72^{\circ}$ となることを見ました。この $\cos 72^{\circ}$ を求めてみます。この値は、【応用】18度の三角比でも求めていますが、以下でも手短に求め方を見ておきましょう。リンク先とは少し異なる方法です。
下のように、 $\mathrm{ PQ=PR }$ の二等辺三角形 PQR を考えます。底角は $72^{\circ}$ で $\mathrm{ QR=1 }$ とします。
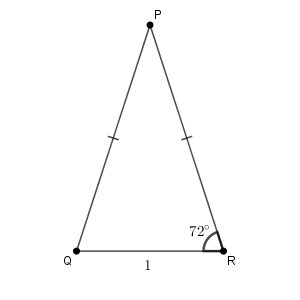
今まで使っていた正五角形とは異なる図形なので点の名前も変えていますが、先ほどの正五角形の頂点を使ってできる三角形 ACD と同じ形になっています。
ここで、 $\angle \mathrm{ PQR }$ の二等分線と辺 PR との交点を S とします。角度を考えると、三角形 PQS も三角形 QRS も二等辺三角形であることがわかります。
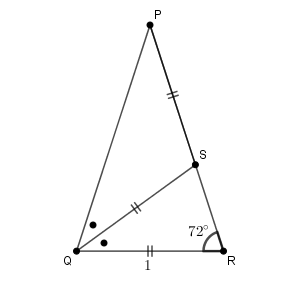
また、角度を考えれば、三角形 PQR と 三角形 QRS が相似になることがわかるので、 $\mathrm{ PQ }=x$ とすると
\begin{eqnarray}
\mathrm{ PQ }:\mathrm{ QR } &=& \mathrm{ QR }:\mathrm{ RS } \\[5pt]
\mathrm{ PQ }\cdot \mathrm{ RS } &=& \mathrm{ QR }^2 \\[5pt]
x (x-1) &=& 1 \\[5pt]
x^2-x-1 &=& 0 \\[5pt]
x &=& \dfrac{1\pm\sqrt{5} }{2}
\end{eqnarray}となります。 $x$ は正なので $\mathrm{ PQ }=\dfrac{1+\sqrt{5} }{2}$ となります。
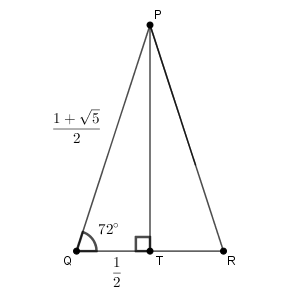
QR の中点を T とすると、
\begin{eqnarray}
\cos 72^{\circ}
&=&
\dfrac{\mathrm{ QT } }{\mathrm{PQ} } \\[5pt]
&=&
\dfrac{\dfrac{1}{2} }{\dfrac{1+\sqrt{5} }{2} } \\[5pt]
&=&
\dfrac{1}{\sqrt{5}+1} \\[5pt]
&=&
\dfrac{\sqrt{5}-1}{(\sqrt{5}+1)(\sqrt{5}-1)} \\[5pt]
&=&
\dfrac{\sqrt{5}-1}{4} \\[5pt]
\end{eqnarray}と求められます。
この結果を使えば、次のようにして、正五角形の一辺の長さが求められます。
正五角形の一辺の長さ再び
$\cos 72^{\circ}=\dfrac{\sqrt{5}-1}{4}$ であることがわかったので、正五角形の一辺の長さの話に戻しましょう。
\begin{eqnarray}
\mathrm{ AB }^2
&=&
2-2\cos 72^{\circ} \\[5pt]
&=&
2-2\cdot \dfrac{\sqrt{5}-1}{4} \\[5pt]
&=&
\dfrac{4-(\sqrt{5}-1)}{2} \\[5pt]
&=&
\dfrac{5-\sqrt{5} }{2} \\[5pt]
\end{eqnarray}となるので、
\begin{eqnarray}
\mathrm{ AB }
&=&
\sqrt{\dfrac{5-\sqrt{5} }{2} } \\[5pt]
&=&
\dfrac{\sqrt{10-2\sqrt{5} }}{2}
\end{eqnarray}と求められます。
ちなみに、「デザインあ おとなスペシャル2020」では、この値がいきなり出てきていましたが、ここにたどりつくには高校1年レベルの内容が必要なので、番組では省略されていたのでしょう。なかなか大変ですが、辺の長さを求めるにはここまでで見た計算が必要となります。
正五角形の作図
さて、半径 $\mathrm{ OA=1 }$ のときに、正五角形の一辺の長さが $\dfrac{\sqrt{10-2\sqrt{5} }}{2}$ になることがわかりました。このことを利用して正五角形の作図をしてみます。こんな複雑な式が本当に作図できるのか信じがたいですが、以下のようにして作図することができます。
点 O をとり、適当な長さの半径で円をかきます。この円周上に点 A をとります。また、 OA を伸ばして円周と交わった点を $\mathrm{ A' }$ とします。
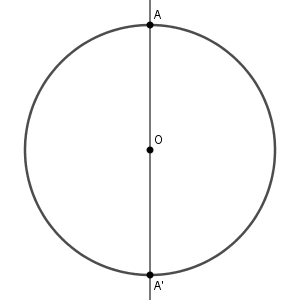
次に $\mathrm{ A, A' }$ を中心とする同じ半径の円をかき、交点を結びます。これは、線分 $\mathrm{ AA' }$ の垂直二等分線を引いていることになります(参考:【基本】垂線二等分線の作図)。
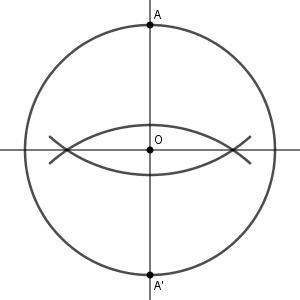
垂直二等分線と円周との交点を F, G とします。そして、F を中心として半径 $1$ の円をかき、もとの円と交わる点を結びます。これは、線分 OF の垂直二等分線を作図していることになります。この直線と OF との交点を H とします。
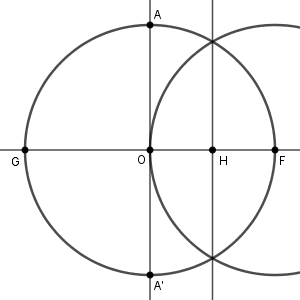
点 H は線分 OF の中点なので、 $\mathrm{ OH }=\dfrac{1}{2}$ です。また、直角三角形 AOH で三平方の定理を使うと
\begin{eqnarray}
\mathrm{ AH }^2
&=&
\mathrm{ AO }^2+\mathrm{ OH }^2 \\[5pt]
&=&
1+\dfrac{1}{4} \\[5pt]
&=&
\dfrac{5}{4} \\[5pt]
\end{eqnarray}となるので、 AH の長さは $\dfrac{\sqrt{5} }{2}$ です。
点 H を中心とし、半径が AH の円をかきます。これと線分 GH との交点を I とします。
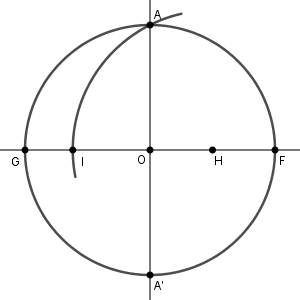
OI の長さは $\mathrm{ HI-OH }=\dfrac{\sqrt{5} }{2}-\dfrac{1}{2}$ となります。直角三角形 AOI に対して三平方の定理と使うと
\begin{eqnarray}
\mathrm{ AI }^2
&=&
\mathrm{ AO }^2+\mathrm{ OI }^2 \\[5pt]
&=&
1+\dfrac{(\sqrt{5}-1)^2}{4} \\[5pt]
&=&
\dfrac{4+(5-2\sqrt{5}+1)}{4} \\[5pt]
&=&
\dfrac{10-2\sqrt{5} }{4} \\[5pt]
\end{eqnarray}となり、 $\mathrm{ AI }=\dfrac{\sqrt{10-2\sqrt{5} }}{2}$ であることがわかります。これは先ほど求めていた正五角形の一辺の長さと一致していますね。つまり、この長さを使って、 A から B, B から C, … と頂点を作図し、線でつなげば正五角形の出来上がり、というわけです。
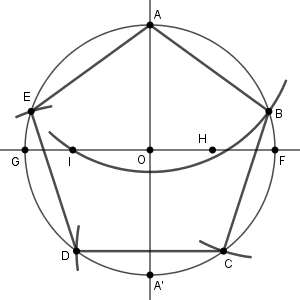
こうして、円に内接する正五角形を作図することができました。
おわりに
ここでは、円に内接する正五角形の作図について見てきました。辺の長さを求めたあと、いろんな線分の長さを求めながら作図方法を見ました。辺の長さは複雑な式でしたが、作図方法自体はそこまで複雑ではないですね。計算ができなければ、なぜこれで作図できているのかがわからず、不思議に感じるかもしれません。





