【発展】2つの直角三角形と2つの角の和の三角比
ここでは、2つの直角三角形を使った特殊な図を考えると、 $\sin (\alpha+\beta)$ といった、2つの角の和の三角比を求めることができる、という話をします。この話は将来別のところで詳しく見るのですが、 $\alpha+\beta$ が鋭角の場合は現時点でも求めることができるので、ここで紹介しておきます。
2つの直角三角形
次のような図を考えてみます。三角形 ABC は、$\mathrm{ AB }=1$, $\angle \mathrm{ B }=\alpha$, $\angle \mathrm{ C }=90^{\circ}$ の直角三角形で、三角形 BCD は、$\angle \mathrm{ B }=\beta$, $\angle \mathrm{ D }=90^{\circ}$ の直角三角形です。
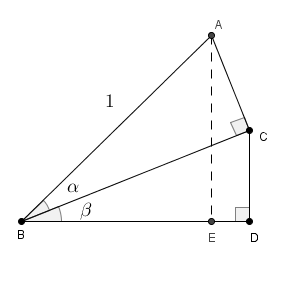
A から BD に下した垂線の足を E とすると、 $\mathrm{ AE }=\sin(\alpha+\beta)$, $\mathrm{ BE }=\cos(\alpha+\beta)$ となります。この長さがどうなるかを考えてみましょう。
といっても、これだけだと求めるのは難しいですね。上の図にさらに追加します。 A から直線 CD へ下した垂線の足を F とします。
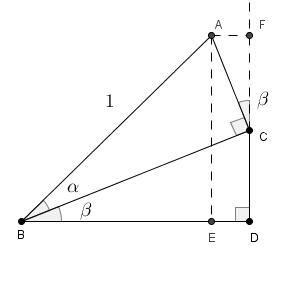
こうすると、 $\angle \mathrm{ CBD }$ も $\angle \mathrm{ ACF }$ も、 $90^{\circ}-\angle \mathrm{ BCD }$ とかけるので、同じ大きさになることが分かります。
さて、 AE の長さを考えてみましょう。これは、 $\mathrm{ CF }+\mathrm{ CD }$ と書けます。 $\mathrm{ AC }=\sin\alpha$ なので、 $\mathrm{ CF }=\sin\alpha\cos\beta$ となります。また、 $\mathrm{ BC }=\cos\alpha$ なので、$\mathrm{ CD }=\cos\alpha\sin\beta$ となります。 $\mathrm{ AE } = \sin(\alpha+\beta)$ だったので、まとめると、次の式が得られます。\[ \sin(\alpha+\beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta \]
また、 BE も同じようにして考えましょう。 BD と AF との差を計算すればいいので、次のように求められます。\[ \cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta \]
これにより、 $\alpha+\beta$ の三角比が、 $\alpha$, $\beta$ の三角比を使って書けることが分かりました。
例
上の2つの式
\begin{eqnarray}
\sin(\alpha+\beta) &=& \sin\alpha\cos\beta + \cos\alpha\sin\beta \\[5pt]
\cos(\alpha+\beta) &=& \cos\alpha\cos\beta-\sin\alpha\sin\beta
\end{eqnarray}が成り立つことを、具体的な値を入れて確認してみます。
【応用】15度の三角比で出てきた、75度の三角比を考えてみましょう。
\begin{eqnarray}
\sin 75^{\circ}
&=&
\frac{\sqrt{6}+\sqrt{2} }{4} \\[5pt]
\cos 75^{\circ}
&=&
\frac{\sqrt{6}-\sqrt{2} }{4}
\end{eqnarray}でしたね。 $75=45+30$ と考えると、
\begin{eqnarray}
\sin45^{\circ}\cos30^{\circ} + \cos45^{\circ}\sin30^{\circ}
&=&
\frac{\sqrt{6}+\sqrt{2} }{4}
\end{eqnarray}なので、 $\sin 75^{\circ}$ と一致します。また、
\begin{eqnarray}
\cos45^{\circ}\cos30^{\circ} -\sin45^{\circ}\sin30^{\circ}
&=&
\frac{\sqrt{6}-\sqrt{2} }{4}
\end{eqnarray}なので、 $\cos 75^{\circ}$ と一致します。よって、この場合でもちゃんと成り立つことが分かりましたね。
おわりに
ここでは、2つの直角三角形を使った特殊な図を使って、 $\sin(\alpha+\beta)$ や $\cos(\alpha+\beta)$ を求めました。これらは、加法定理と呼ばれるもので、三角関数の分野で将来詳しく学びます。ただ、現時点でも、いろんな線分の長さを使えば求められるので、ここで紹介しておきました。





