【応用】実数条件と領域
ここでは、領域を求めるときに、実数条件を考える問題を見ていきます。
実数条件と領域
u, v が実数なのだから、 x, y も実数です。しかし、すべての実数をとるとは限りません。【応用】通過領域(存在条件)で見たように、対応する u, v があるかどうかを考えなくてはいけません。
例えば、 $x=0,y=1$ とすると、これに対応する u, v はどうなるでしょうか。和が $0$ なので、 $v=-u$ となります。よって、 $y=uv=-u^2$ となります。これが $1$ になることはありません。つまり、対応する実数 $(u, v)$ の組合せがない、ということです。なので、こうした点は除かなくてはいけません。
さて、問題は、どのようにして「対応する実数 u, v が存在する」条件を考えるか、です。
「実数が存在する」という条件は今まであまり出てきたことがありませんが、似たものとして、「実数解が存在する条件」は出てきました。二次方程式の判別式が0以上、という条件ですね。しかし、二次方程式は今ありません。
ただ、よく見ると、 x は和、 y は積となっていますね。この形と「二次方程式」というワードから、【基本】二次方程式の解と係数の関係との関連を考えてみましょう。
ある二次方程式の解が $u,v$ だったとしましょう。二次の項の係数が $1$ だとすると、一次の項の係数は $-(u+v)$ なので、 $-x$ と一致します。また、定数項は $uv$ なので、 $y$ と一致します。このことから、 $u,v$ は\[ t^2-xt+y=0 \]という t に関する二次方程式の解となります。こうした考えは、【標準】解から二次方程式を作るとも関連しています。
u, v に対して x, y を対応させるのは簡単ですね。和と積を計算すれば終わりです。一方、 x, y から u, v を求めるのは簡単ではありません。しかし、このように、解と係数の関係を用いれば、二次方程式を解くことによって、 x, y から u, v を対応させることができる、ということなんですね。
これを使えば、 x, y について、対応する実数 u, v が存在するかどうかは簡単にわかります。\[ t^2-xt+y=0 \]が実数解を持つ条件を考えればいいからです。よって、判別式が $0$ 以上ならいいので
\begin{eqnarray}
(-x)^2 -4y \geqq 0 \\[5pt]
y \leqq \frac{1}{4}x^2 \\[5pt]
\end{eqnarray}となります。よって、求める領域は以下のようになります。
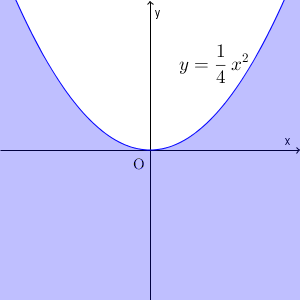
図の色で塗った部分(境界線上の点を含む)となります。なお、上で見た通り $(0,1)$ は含まれていませんね。
ここで見たような「対応する実数が存在する条件」のことを、「実数条件」と呼ぶことがあります。
実数条件と領域その2
これも、先ほどと同様に、実数 u, v が存在するための条件を考える必要があります。実数
u, v が存在することは、 $t^2-xt+y=0$ が実数解を持つことと同値であり、上で見た通り\[ y \leqq \frac{1}{4}x^2 \]を満たすことと同値です。
また、 $u^2+v^2\leqq 1$ という条件も、 x, y を使って表しましょう。【標準】対称式の値を参考に、 $x=u+v$ を2乗して余分な部分を引く、と考えて
\begin{eqnarray}
u^2+v^2 & \leqq & 1 \\[5pt]
(u+v)^2-2uv & \leqq & 1 \\[5pt]
x^2-2y & \leqq & 1 \\[5pt]
y & \geqq & \frac{1}{2}x^2-\frac{1}{2} \\[5pt]
\end{eqnarray}が得られます。
2つの条件を満たさないといけないので、この両方に含まれる部分が答えとなります。
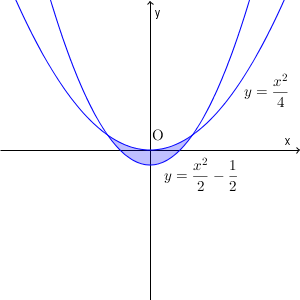
図の色で塗った部分(境界線上の点を含む)となります。
おわりに
ここでは、領域を求めるときに、実数条件を考える問題を見てきました。例題1を見てから例題2を見れば実数条件を考えないといけないことには気づきやすいですが、いきなり例題2だけを見た場合には忘れやすいです。
問題文には「実数」と書いているだけです。よくある条件なので、スルーしてしまいがちです。「対応する実数が存在するか」という点に自分で気づかないといけません。





