【応用】二次曲線の極方程式

ここでは、二次曲線の極方程式を見ていきます。

二次曲線の極方程式

【応用】二次曲線と離心率で離心率について見ました。離心率を使うと、二次曲線を包括的に扱うことができます。

どういう内容だったかを書いておきます。点 $\mathrm{F}$ からの距離と、 $\mathrm{F}$ を通らない直線 $\ell$ からの距離の比が $e:1$ となる点 $\mathrm{P}$ の軌跡を考えます。すると、 $e$ の値によって、以下のようになります。

• $0\lt e\lt 1$ のとき、楕円となる。焦点の1つは点 $\mathrm{F}$ である。
• $e=1$ のとき、放物線となる。焦点は点 $\mathrm{F}$ である。
• $e\gt 1$ のとき、双曲線となる。焦点の1つは点 $\mathrm{F}$ である。

この $e$ のことを離心率というのでした。これを踏まえて、二次曲線の極方程式を考えてみましょう。

上で $\mathrm{F}$ と呼んでいた点は、極 $\mathrm{O}$ とすることにします。また、直線 $\ell$ は、 $(a,0)$ を通り、始線に垂直な直線としましょう（ $a\gt 0$ ）。そして、点 $\mathrm{P}$ が条件を満たすとします。

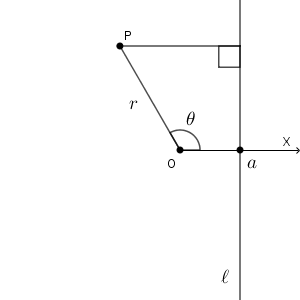
こうすると、極 $\mathrm{O}$ からの距離は $r$ です。また、直線 $\ell$ からの距離は $a-r\cos\theta$ です。なので、距離の比が $e:1$ なら、次のような関係式が成り立ちます。\[ r:(a-r\cos\theta)=e:1 \]これを変形すると
\begin{eqnarray} r &=& e(a-r\cos\theta) \\[5pt] r(1+e\cos\theta) &=& ae \\[5pt] r &=& \frac{ae}{1+e\cos\theta} \\[5pt] \end{eqnarray}となります。これが二次曲線の極方程式です。

• $0\lt e\lt 1$ のとき、楕円を表す。焦点の1つは極 $\mathrm{O}$ である。
• $e=1$ のとき、放物線を表す。焦点は極 $\mathrm{O}$ である。
• $e\gt 1$ のとき、双曲線を表す。焦点の1つは極 $\mathrm{O}$ である。

二次曲線の性質

次の問題を考えてみましょう。

これは、極方程式で考えると扱いやすくなります。

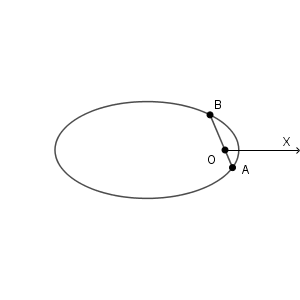
極 $\mathrm{O}$ を焦点とする楕円を考えると、\[ r=\frac{ae}{1+e\cos\theta} \]と書くことができます。ここで、 $a,e$ は定数で、 $0\lt e\lt 1$ です。

$\mathrm{A}(r_a,\theta_a)$, $\mathrm{B}(r_b,\theta_b)$ とすると、 $\theta_b=\theta_a+\pi$ となるので（ $2\pi$ の整数倍は無視する）、
\begin{eqnarray} \frac{1}{r_a}+\frac{1}{r_b} &=& \frac{1+e\cos\theta_a}{ae}+\frac{1+e\cos\theta_b}{ae} \\[5pt] &=& \frac{1+e\cos\theta_a}{ae}+\frac{1-e\cos\theta_a}{ae} \\[5pt] &=& \frac{2}{ae} \end{eqnarray}となり、 $a,e$ のみを含む式だから、一定の値であることがわかります。

これを直交座標で示すのは面倒ですが、極座標の場合は極（ここでは焦点）からの距離と角度をメインに考えられるので、この問題のような場合にはだいぶ計算が楽になります。

また、よく見ると、 $e$ の値の大きさを使っていないことがわかります。つまり、これは楕円について成り立つだけでなく、放物線、双曲線でも同じ性質が成り立ちます。

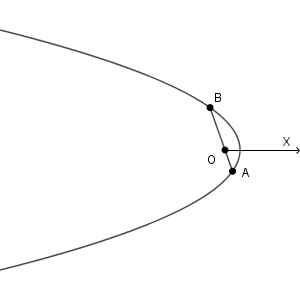
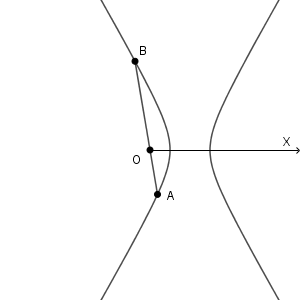
同じ形の式で表現できるので、全部まとめて扱えるんですね。

おわりに

ここでは、二次曲線の極方程式について見てきました。一般的な形を見た後に、二次曲線の性質も見ました。極座標を使うよさが感じられると思います。